Chunk Decomposition in Anagram Solving Tasks


Опубликована Авг. 23, 2019
Последнее обновление статьи Авг. 23, 2022
Abstract
If a well-known word is a part of an anagram stimulus, it may complicate the process of solving the anagram. This may happen because a word inside the anagram may serve as a semantic prime, or because such a word is a chunk that is difficult to decompose. We manipulated the structural features of word and nonword chunks in anagram stimuli to find out which features of a chunk, semantic or structural, are more influential in anagram solving. The results showed that the semantic but not the structural features of a chunk are more important for five-letter anagrams, while none of these features are crucial for solving six-letter anagrams. We suggest that different mechanisms underlie the solution process of shorter five- letter and longer six-letter anagrams. Limitations of the study and its implications for future research are discussed.
Ключевые слова
Anagram solving, structural features of a chunk, semantic features of a chunk, chunk decomposition
Introduction
When solving an anagram, a person tries to rearrange letters to get a new representation, and then probes her/his vocabulary for a match (Richardson & Johnson, 1980). Three groups of factors influence this process. The evidence for semantic influences was obtained mainly from studies that utilized different priming techniques (Dom- inowski & Ekstrand, 1967; White, 1988). Other studies demonstrated that anagrams are more difficult to solve when they are presented as other meaningful words (Ekstrand & Dominowski, 1968). The latter studies imply that if anagram stimuli contain another well-known word, it may function as a semantic prime itself. The second group of factors includes different structural features of anagrams. Structural features fall into several different categories: lexical features (especially word frequency; Dominowski, 1967), orthographical features (including bigram frequency; Dominowski, 1967), letter moves needed to solve an anagram (Dominowski, 1966), letter transition probabilities (Beilin & Horn, 1962), and phonological features (such are easiness of pronunciation: Fink & Weisberg, 1981; and number of syllables: Adams, Stone, Vincent, & Muncer, 2011). The third group of factors includes individual differences concerning vocabulary capacity (Mendelsohn, Griswold, & Anderson, 1966), skills in anagram solving (Novick & Sherman, 2003), and reading proficiency (Henin, Accorsi, Cho, & Tabor, 2009). These factors interact with each other (Mendelsohn, 1976; Gilholly & Johnson, 1978; Novick & Sherman, 2008), making the assessment of anagram difficulty an extremely complex task.
A mainstream theory of anagram solving states that the process of searching for a solution is governed by implicit knowledge of the statistical properties of a language: a solver tries to combine letters in sequences that are more common in his/her vocabulary (Gilholly & Johnson, 1978; Richardson & Johnson, 1980). The three groups of factors discussed above make the process of finding a solution more or less difficult.
Another theoretical framework is presented in theories of insight problem solving. According to Ohlsson’s impasse-insight theory, an impasse in insight problems occurs because of a non-optimal representation of a task based on prior knowledge the solver needs to overcome. Two mechanisms of representation change are proposed: constraint relaxation and chunk decomposition (Knoblich, Ohlsson, Haider, & Rhenius, 1999). In recent publications, Chistopolskaya and Lazareva (Chistopolskaya, Lazareva, Markina, & Vladimirov, 2019; Lazareva, Chistopolskaya, & Akatova, 2019) stress that constraint relaxation is described as a high-level cognitive process, while chunk decomposition is viewed as a low-level perception process. They propose an elaboration of the theory by introducing a low-level process of perception constraint relaxation, and a high-level process of semantic chunk decomposition.
Although theories of insight solution are often tested via anagram solving (see Ellis, Glaholt, & Reingold, 2011 for a brief review), some authors argue that anagrams are not insight problems at all (Weisberg, 1995), and others even use anagram solution tasks as control tasks in studying insight solutions (e. g., Ollinger, Jones, & Knoblich, 2008). Indeed, the solution of an anagram is not always a pop-up insight solution, and researchers often use some measures of subjective experience of insight during the solution process in anagram solution studies. Moreover, there is an ongoing discussion as to whether there are specific insight- related processes, or pop-up and analytical decisions are based on the very same processes (Weisberg, 2015). Therefore, theories of insight problem solving may be useful in studying the anagram solution process, but should be considered with certain cautions and limitations.
The scope of our study is anagram solution, not insight problem solving. Nevertheless, the importance of structural and semantic features of anagram stimuli is also emphasized in insight-related anagram solution studies. For example, Ellis and Reingold (2014) suppose that an impasse in an anagram solution is a result of “orthographic, phonological, lexical, and/or semantic activation” (p. 670). In their study, they used five-letter anagrams with one added distraction letter as experimental stimuli. Stimuli were presented as a three-letter chunk in the middle of a screen surrounded by three other letters. The chunk in the middle could be a word or a nonword — a meaningless set of three letters. Participants needed more time to solve an anagram if the chunk in the middle was a word. What remains unclear is which properties of the chunk make the decision more difficult. Indeed, three-letter nouns also consist of bigrams of high frequency and are syllables that are easy to pronounce. In our study, we try to answer the question: What features of a chunk make an anagram solution task more difficult to solve: semantic or structural? We approach the question by controlling some structural features of the nonword chunks as part of the anagram stimuli (Lapteva, 2016).
Finally, we should point out that when we speak about the semantic features of a chunk, we consider it in a broader sense than the term “semantic chunk” proposed by Chistopolskaya and Lazareva (Chistopolskaya, Lazareva, Markina, Vladimirov, 2019), which has a specific meaning in the context of the impasse-insight theory. The question we try to answer is consistent with different theoretical frameworks. Our goal is not to test a particular theory or theories, but to find some empirical evidence that can be useful for the further development of theories concerning anagram solving.
Materials and Method
Participants
Forty five undergraduate students from Samara University (33 women) volunteered in the study. All participants had normal or corrected to normal eyesight and were native Russian speakers.
Materials
Twenty one five-letter and 24 six-letter high frequency Russian nouns were selected from the frequency dictionary of Russian vocabulary by Lyashevskaya and Sharov (2009) as solutions to the anagram problems. Each word was the only meaningful word possible to construct from its letters, and each word contained at least one set of three letters that can be arranged into a three-letter meaningful word. Each anagram followed the pattern “X-YYY-X” for five-letter words or “X-YYY-XX” for six-letter words. Three types of anagrams were created for every word. In the word type of anagrams (W anagram), the “YYY" section comprised a meaningful three-letter word. In the pseudoword type of anagrams (PW anagram), “YYY" is a well-pronounced sequence of consonant-vowel-consonant (or vowel - consonant-vowel in some cases for the six-letter anagrams). In the nonword type of anagrams (NW anagram), “YYY” are three consonants that are difficult to pronounce in sequence. For example, for the word “TOWEL”, “E-LOT-W” is a W-anagram, “E-WOL-T” is a PW-ana- gram, and “O-LWT-E” is a NW-anagram. All five-letter target words consisted of two syllables and had only two vowels, fifteen six-letter target words consisted of two syllables and contained two vowels also, and the remaining nine six- letter words consisted of three syllables and contained three vowels. To balance the difficulty of anagrams, none of the first and last letters of the solution words were in their correct position in any of the anagrams.
Procedure
The experiment was programmed as a script in PsychoPy v. 1.90.2 software (Peirce, 2019). Stimuli were presented in capital letters on a laptop screen. “YYY" chunks were highlighted in green and were separated from the other letters by single spaces. The three sets of stimuli were composed using a Latin square. Each participant had to solve tasks for each type of five-letter anagram and 8 tasks for each type of six-letter anagram (45 tasks in total). Each task was presented for 1 minute only. Participants were told to press the space bar when they solved the task and to say the answer aloud. In very rare and sporadic cases of a wrong
answer, the experimenter said “Wrong!” to the participants, and they continued to try to solve the anagram until finding the correct solution or until the minute expired. Because such situations were rare, we analyzed the times of correct decisions only. Each participant completed five practice tasks before the main procedure. Practice results were not recorded or analyzed.
Results and Discussion
Difficulty Balance Checks
When constructing our stimuli, we controlled for difficulty of pronunciation. Other structural features of anagrams that are important are bigram frequency and solution frequency. Studying the differences between certain structural features is not within the scope of the present study, but we tried to ensure that the frequencies of bigrams in different types of stimuli varied in accordance with differences in pronunciation.
Mean frequency of the bigrams in the “YYY” chunks did not differ in the W and PW anagram conditions, both in their instances per million words and their ranked order (for neither five- nor six-letter anagrams; p > .65 for all t-test pairwise comparisons between W and PW anagrams). In contrast, both instances per million words were lower and ranked order was greater for NW anagrams than for W and PW anagrams (pc.001 for all comparisons). Instances per million words and ranked order did not differ between the five and six-letter solutions of anagrams (p > .69 for all comparisons).
For six-letter anagrams, the bigram frequencies of the last two letters, which can also be viewed as a chunk with no semantic meaning in all types of anagrams, do not differ (F(2,69) = 1.38; p = .26 for instances per million words, and F(2,69) = .55; p = .581 for ranked order).
Thus, when we speak about the structural features of anagrams in our study, we refer to the joint effect of pronunciation and bigram frequency.
Among six-letter anagram solutions, three-syllable words are a bit more frequent than two-syllable words: t(22) = 2.09, p = .049 for instances per million words, and t(22) = 1.56, p = .133 for ranked order.
Main Results
Statistical analysis was conducted in the R software environment (R Core Team, 2019). The descriptive statistics of the raw data for all experimental conditions are presented in Table 1. Participants solved 71.7% of five-letter W anagrams, which is significantly less than the number of the correct solutions for the PW anagrams (81.6 %; x2(l) =8.0; p = .009) and NW anagrams (82.5%; y2(l) = 9.8; p = .005). The solving rate was much lower for six-letter anagrams than for five-letter ones. Participants solved 46.1 % of six- letter W anagrams and 51.9% of both PW and NW six- letter anagrams (no significant differences between them: X2(2)=3.3;p = .195).
To analyze decision times, we conducted a mixed models analysis using the lme4 R package (Bates, Maehler, Bolker, & Walker, 2015). This statistical method is relatively new, and may need some clarifications. Our data are multilevel and consist of multiple observations for multiple participants. The traditional approach to analyzing such data is to use ANOVA after averaging across participants (Fl analysis) or across observations (F2 analysis). Shortcomings of such averaging are straightforward: we lose some data that may be informative, and our effect size estimations become dependent on the number of observations (in Fl analysis) or number of participants (in F2 analysis). Mixed methods allow explicit modeling variation between participants and between stimuli as random effects simultaneously, without any averaging. As a result, there are several benefits of mixed models over traditional ANOVA approaches: they model the structure of the data more precisely, they can handle heteroscedas- ticity of the data, they are more robust to overfitting; and they are more powerful (Chetverikov, 2015; Baayen, 2012). Interpretation of the fixed effects, which are usually of interest for a researcher, is very similar to the traditional ANOVA.
We entered anagram type and anagram length as fixed effects, and participant ID and anagram solution as random effects. P-levels for main effects and their interaction were obtained by Satterthwaite’s method of degrees of freedom approximation using the ImerTest R package (Kuznetsova, Brockhoff, & Christensen, 2017). Decision times were analyzed only for solved anagrams.
Mixed models require residuals to be normally distributed. We followed the guidelines of Gurka, Edwards, Muller, and Küpper (2006) and analyzed total residuals using quantile-quantile plots. Solution times were box-cox transformed before the analysis to obtain normal distribution of total residuals (X = .101
We found significant main effects for both anagram length (F(l, 40.91) =0.93; pc.001) and anagram type (F(2,44.24) =4.09; p = .O24). Factor interaction significance was very close to the conventional threshold of .05 (F(2,44.17) = 3.03; p = .058). Pairwise
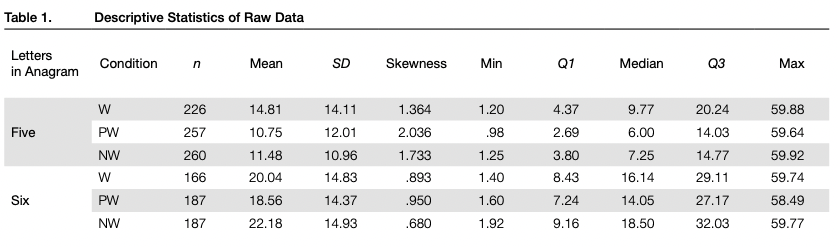
Table 2. Least Squares Estimates of Means and Confidence Intervals for Box-Cox Transformed Data
Letters in Anagram | Condition | Mean | SE | df | 95 % conf. int. | |
lower | upper | |||||
| W | 2.75 | .16 | 48.25 | 2.44 | 3.07 |
Five | PW | 2.22 | .16 | 48.86 | 1.90 | 2.54 |
| NW | 2.36 | .12 | 53.59 | 2.12 | 2.61 |
| W | 3.31 | .16 | 58.54 | 2.99 | 3.63 |
Six | PW | 3.16 | .16 | 58.90 | 2.84 | 3.49 |
| NW | 3.39 | .13 | 69.09 | 3.13 | 3.65 |
comparisons1 (Here and thereafter, Kenward-Roger approximation of degrees of freedom and Tukey FWER correction were used in all pairwise comparisons in mixed effect models.) revealed that the main effect of anagram type yielded significant differences between five-letter anagrams only. Five-letter W anagrams needed more time to be solved than both PW anagrams (t(3.24) = 3.24; p = .030) and NW anagrams (t(31.7) = 3.01; p = .053), while time to solve PW and NW anagrams was close (t(33.9) = 1.00; p = .916). For six-letter anagrams, p > .65 for all pairwise comparisons between anagram types. Least squares estimations of means and confidence intervals are presented in Table 2. Note that although these statistics are the most appropriate to estimate effect sizes, back-transformed means do not correspond to the means of raw data any longer (for details, see Section 3.2 of Hyndman & Athanasopoulos, 2018).
For six-letter anagrams, we tested an additional model, entering number of syllables and anagram type as fixed effects, and keeping participant ID and anagram solution as random effects. Neither main effect of number of syllables (F(l, 20.03) = .01;p = .919) nor factor interaction (F(2,518.01) = 1.15; p = .317) was significant.
Preliminary Discussion
Difficulty balance checks for “YYY” chunks provided some evidence that W and PW anagrams are alike in structure and should be about equally difficult to decompose, while NW anagrams are structurally different. We have also found evidence that five-letter anagrams are harder to solve if they contain a semantically meaningful chunk, but this is not true for six-letter anagrams: neither the number of solved anagrams nor solution times differed significantly between different types of six-letter anagrams. There was no evidence that the structural features of chunks influenced anagram task difficulty for either the five- and six- letter anagrams.
One possible explanation for the lack of significant differences between W and other types of six-letter anagrams is that six-letter anagrams are harder to solve in general. We know this because fewer of the six-letter anagrams were solved, and it required significantly more time to solve them. This implies the possibility that semantic differences are more important for solving easier anagrams and less important for more difficult ones. We can test this possibility by splitting all the tasks by the median decision time and assuming anagrams with decision times below the median are easier tasks, and anagrams with decision times above the median are more difficult tasks. We hypothesize that for the easier five-letter anagrams the effect of semantic features of a chunk would be greater than for anagrams that are more difficult. We also hope to find evidence that among the easier six-letter anagrams W variants are more difficult to solve than PW and NW variants.
There is an issue about which median is more appropriate when splitting the data: should we use the one grand median across all participants, or different medians for each participant respectfully? We chose the latter variant for two reasons. First, the solution difficulty of the very same anagram may vary across participants, and using different medians for different participants borrows the same rationale as participant random effects in mixed models. Second, it yields to a more balanced design, when an equal amount of measures for each participant is assigned to the groups of more difficult and easier solutions2 (In fact, the division anagram solution tasks into two groups by grand median produce very similar results to the division by medians computed for each participant separately (φ = .66 for five-letter anagrams, and φ = .76 for six-letter anagrams). We repeated the analyses discussed below using the grand median as division criterion, and the results were quite similar and thus not reported in the article.).
Exploratory Results
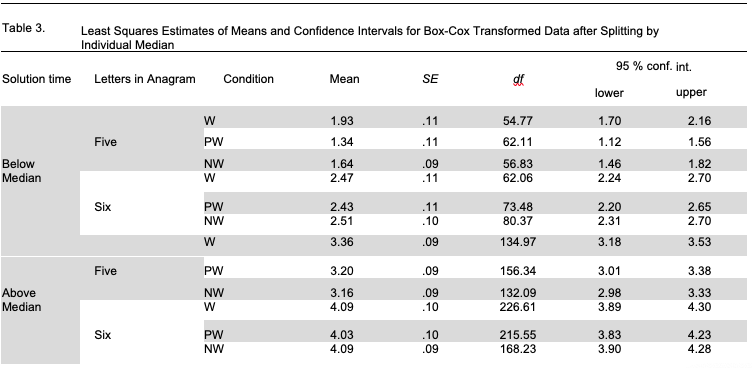
We conducted mixed models analysis separately for five- and six-letter anagram tasks, entering anagram difficulty and anagram type as fixed effects, and participant ID and anagram solution as random effects. For five-letter anagram tasks, the interaction of fixed effects was significant (F(2,698.1) =3.49; p = .O31). Pairwise comparisons showed that the main effect of anagram type holds for easier anagram tasks, but is not significant for tasks that are more difficult. For easier five-letter anagrams, the solution time was significantly longer for W anagrams than for PW anagrams (t(694) =3.14; p = .002) but not significantly longer for NW anagrams (t(691)=2.31; p = .123). Surprisingly enough, solution time was also longer for NW anagrams than for PW anagrams (t(691)=2.81; p = .058). For more difficult five-letter anagrams, W anagrams needed a bit more time to be solved than PW and NW anagrams, but none of the pairwise comparisons was significant (t(691) = 1.74;p = .5O6 for W and PW comparison; t(689) = 2.37; p = .169 for W and NW comparison; t(690) = .53; p = .995 for PW and NW comparison). For six-letter anagrams, the factor interaction was not significant (F(2,466.4) =0.39; p = .676), nor were the pairwise comparisons between anagram types for both levels of difficulty (p > .9 for all pairwise comparisons). Least squares estimations of means and confidence intervals are presented in Table 3.
Preliminary Discussion of Exploratory Results
Our hypothesis about solution time holds true for five-letter anagrams but not for six-letter anagrams. Due to the reduced sample size in our exploratory analysis (because the number of anagram tasks reduced two times for each type of anagram), these results should be interpreted with caution.
General Discussion
The goal of our study was to find out which features of a chunk in the anagram solution tasks (namely, semantic or structural) make it more difficult to decompose, causing the task to be more difficult. The structural difficulty of chunks was manipulated as a frequency of bigrams in a chunk, combined with its pronounceability. In these terms, W and PW anagrams were structurally equal, and differed from NW anagrams. We found no evidence that structural features influenced the difficulty of the anagram solving task in both preplanned and exploratory analyses, thus failing to replicate the results from previous research (Dominowski, 1967; Gilholly & Johnson, 1978). One possible explanation is that our study is underpowered. Power analysis for mixed effects models is complicated, because there is an ongoing discussion about which effect size measures are most appropriate for such models (Rights & Sterba, 2019), and the most common practice is to run simulations (Brysbaert & Stevens, 2018). We did not perform such simulations prior to our study.
Meanwhile, we did find evidence for meaningful chunks making five-letter anagrams more difficult to solve across all analyses. Even if our study is indeed underpowered, the robustness of effects of the chunk semantic features across all mixed models ran for five-letter anagrams make these effects paramount.
Compared to this result, our failure to find any evidence of chunk semantic features influence on six-letter anagram task solution implies the possibility that the processes of solving five or six-letter anagrams are somehow different. At this point, we can only speculate what these differences are. One possible explanation concerns the role of working memory in the process of anagram solving. Once all the chunks of an anagram are decomposed, a solver has to keep all the letters active in working memory simultaneously. In case of six-letter anagrams, it may lead to working memory overload, in its turn, leading to generation of new chunks or returning to previously decomposed ones, and negate the effects of chunk decomposition. This proposition is still highly hypothetical and needs to be further elaborated.
In a recent study with a highly similar design, Lazareva, Chistopolskaya and Akatova (2019) used six-letter anagrams in which the first three letters formed a meaningful word or were meaningless. The difference between the cited study and ours is that we also delineated between PW and NW anagrams, and we positioned meaningful or meaningless chunks not at the beginning but in the middle of our anagram stimuli. Furthermore, Lazareva and colleagues also measured subjective experiences of insight, awareness of the word at the beginning of anagram stimuli, and dwells in eye movements for each decision. In the second experiment, they separated the chunk at the beginning of the anagram by space and color similar to Ellis and Reingold (2014) and our study. In line with our results, Lazareva et al. did not find significant differences in solution times and the quantity of solved anagrams in the second experiment. Nevertheless, there were such differences in the first experiment, in which anagrams were presented in a usual way, without color highlighting and space separation. Most of the participants did not notice a word at the beginning of anagram stimuli in the first experiment, but were consciously aware of it in the second experiment. These results imply that conscious awareness about the meaningful chunk in anagram stimuli may help participants to overcome a fixation. In our study, participants needed about twice as long to solve six-letter anagrams than five-letter ones. It is possible that, in the case of five letter anagrams, they often reached a decision before consciously noticing a meaningful word as part of the anagram. To summarize, conscious awareness of the semantic features of a chunk may play an important role in the anagram solution process.
There are certain limitations of our study. Although six-letter anagrams are more complex and need more time to be solved, participants had equal time allowances for five- and six-letter anagrams. Thus, our results may suffer from a ceiling effect. If participants took more time to solve the six-letter anagrams and solved more of those tasks, it is possible that the effects we were looking for become more salient.
We controlled three-letter chunk frequency by frequencies of the bigrams in its composition. Nevertheless, it is more likely that the difficulty of a three-letter chunk is more determined by the frequency of the whole sequence. To our knowledge, there are no publicly accessible frequency tables for three-letter sequences in the Russian language. Thus, we did the best we could do with what was available.
Skills in anagram solving can be another factor that contaminated our results. Novick and Sherman (2008) found evidence that pronounceability is more important for participants with low skills in anagram solving, while structural characteristics have more impact for skillful solvers. We did not measure any individual difference factors. Such individual differences are another potential cause of our failure to find evidence for the influence of structural features of chunks on anagram solving.
It is known that decision times for pop-out solutions are usually smaller than for incremental solutions (Novick & Sherman, 2003). It is plausible that the chunk features of interest in our study differ in their importance for anagram solving, if the solution is insight-like (pop-out) or not, but not if the anagram itself is harder or easier to solve. In our study, we did not measure whether the decisions were pop-out or incremental. However, in the cited study by Lazareva et al. (2019), subjective experience of insight was measured and reported in the first experiment, and the authors did not find differences between anagrams that contained a shorter three-letter word and those that contained a meaningless sequence of three letters.
Conclusions
Taking into consideration all the limitations of the present study, one should view our results as preliminary. If semantic fixedness occurs, it becomes the main difficulty to overcome when solving short, five-letter anagrams, while the structural features of a chunk are not of great importance. Solving longer, more complex anagrams likely relies upon different mechanisms, for which the semantic features of chunks in the anagram are of less significance. We suggest that differences in the processes of solving shorter and longer anagrams are related to working memory operation and overload. We also suggest that conscious awareness about the semantic features of anagram stimuli may help solvers to overcome fixedness on them.
References
Adams, J. W., Stone, M., Vincent, R. D., & Muncer, S.J. (2011). The role of syllables in anagram solution: A Rasch analysis. The Journal of General Psychology, 138(2), 94-109. dot: 10.10 80/00221309.2010,540592
Baayen, R.H. (2012). Mixed-effect models. In A. C. Cohn, C. Fougeron, & M. K. Huffman (Eds.), The Oxford handbook of laboratory phonology (pp. 668-677). New York, NY: Oxford University Press. doi:10.1093/oxfordhb/ 9780199575039.001.0001
Bates, D., Maehler, M., Bolker, B., & Walker, S. (2015). Fitting linear mixed-effects models using lme4. Journal of Statistical Software, 1(1), 1-48. Retrieved from https://www.jstatsoft. org/v067/i01 doi:10.18637/jss.v067.i01.
Beilin, H., & Horn, R. (1962). Transition probability effects in anagram problem solving. Journal of Experimental Psychology, 63(5), 514-518. doi:10.1037/h0042337
Brysbaert, M., & Stevens, M. (2018). Power analysis and effect size in mixed effects models: A tutorial. Journal of Cognition, 1(0. 9:1-20. doi:10.5334/joc.l0
Chetverikov, A. A. (2015). Linear mixed effects regression in cognitive studies. The Russian Journal of Cognitive Science, 2(1), 41-51. (In Russian). Retrieved from http://cogiournal. org/2/l/pdf/ChetverikovRICS2015.pdf.
Chistopolskaya, A. V., Lazareva, N.Y, Markina, P.N., & Vladimirov, I.Y. (2019). The concept of high-level and low-level processes in cognitive psychology. S. Olsson’s representational change theory from the position of the level approach. Vestnik YarGU. Seriya Gumanitarnye Nauki [The Bulletin of P. G. Demidov Yaroslavl State University. Series Humanities], 49(3), 94-101. (In Russian).
Dominowski, R. L. (1966). Anagram solving as a function of letter moves. Journal of Verbal Learning and Verbal Behavior, 5(2), 107-111. doi:10.1016/S0022-5371(66)80002-6
Dominowski, R.L. (1967). Anagram solving as a function of bigram rank and word frequency. Journal of Experimental Psychology, 75(3), 299-306. doi:10.1037/h0025060
Dominowski, R.L., 8r Ekstrand, B.R. (1967). Direct and associative priming in anagram solving. Journal of Experimental Psychology, 74(1), 84-86. doi:10.1037/h0024509
Ekstrand, B. R., & Dominowski, R. L. (1968). Solving words as anagrams: II. A clarification. Journal of Experimental Psychology, 77(4), 552-558. doi:10.1037/h0026073
Ellis, J. J., Glaholt, M. G., & Reingold, E.M. (2011). Eye movements reveal solution knowledge prior to insight. Consciousness and Cognition, 20(3), 768-776. doi:10.1016/j. concog.2010.12,007
Ellis, J. J., & Reingold, E.M. (2014). The Einstellung effect in anagram problem solving: Evidence from eye movements. Frontiers in Psychology, 5,679:1-7. doi: 10.3389/fpsyg.2014,00679 Fink, T. E., & Weisberg, R. W. (1981). The use of phonemic information to solve anagrams. Memory and Cognition, 9(4), 402-410. doi: 10.3758/bf03197566
Gilhooly, K.J., & Johnson, C.E. (1978). Effects of solution word attributes on anagram difficulty: A regression analysis. Quarterly Journal of Experimental Psychology, 30(1), 57-70. doi: 10.1080/14640747808400654
Gurka, M. J., Edwards, L. J., Muller, К. E., & Küpper, L. L. (2006). Extending the Box-Cox transformation to the linear mixed model. Journal of the Royal Statistical Society: Series A (Statistics in Society), 169(2), 273-288. doi:10.111 l/j.l467-985X,2005.00391.x
Henin, J., Accorsi, E., Cho, P., & Tabor, W. (2009). Extraordinary natural ability: Anagram solution as an extension of normal reading ability. In Proceedings of the 31st Annual Meeting of the Cognitive Science Society (pp. 905-910). Mahwah, New Jersey: Lawrence Erlbaum. Retrieved from http://csiarchive. cogsci.rpi.edu/Proceedings/2009/papers/158/paperl58.pdf.
Hyndman, R.J., & Athanasopoulos, G. (2018). Forecasting: Principles and Practice. OTexts: Online publication. Retrieved from https://otexts.com/fpp2/.
Knoblich, G., Ohlsson, S., Haider, H., & Rhenius, D. (1999). Constraint relaxation and chunk decomposition in insight problem solving. Journal of Experimental Psychology: Learning Memory, and Cognition, 25(6), 1534-1555. doi:10.1037/0278-7393.25.6.1534
Kuznetsova, A., Brockhoff, P. B., & Christensen, R. H. B. (2017). ImerTest package: Tests in linear mixed effects models. Journal of Statistical Software, 82(13), 1-26. doi:10.18637/jss. Ѵ082.І13
Lapteva, E.M. (2016). Eye movements as indicator of solution knowledge in anagram solving. Experimental Psychology (Russia), 9(3), 41-53. doi:10.17759/exppsy.2016090304
Lazareva, N.Y, Chistopolskaya, A. V, & Akatova, N.Y. (2019). Investigation of semantic chunk decomposition on anagrams. In E. V. Pechenkova, 8r M. V. Falik- man (Eds.), Cognitive Science in Moscow: New research. Conference proceedings 19 of June 2019
(pp. 301-305). Moscow: Buki Vedi, IPPiP. (In Russian). Retrieved from http://conf.virtualcoglab.ru/2019/ Pro ceedings/pdf/LazarevaetalMosco wCogSci2019.pdf.
Lyashevskaya, O.N., & Sharov, S.A. (2009). Frequency dictionary of contemporary Russian language (based on National corpus of Russian language). Moscow: Azbukovnik (In Russian). Retrieved from http://dict.ruslang.ru/freq.php.
Mendelsohn, G.A. (1976). An hypothesis approach to the solution of anagrams. Memory and Cognition, 4(5), 637-642. dfiuia3Z5SZBEQ321322S
Mendelsohn, G. A., Griswold, В. B., & Anderson, M. L. (1966). Individual differences in anagram-solving ability. Psychological Reports, 19(3), 799-809. doi:10.2466/pr0.1966.19.3.799
Novick, L.R., & Sherman, S.J. (2003). On the nature of insight solutions: Evidence from skill differences in anagram solution. The Quarterly Journal of Experimental Psychology Section A, 56(2), 351-382. doi:10.1080/02724980244000288
Novick, L.R., & Sherman, S.J. (2008). The effects of superficial and structural information on online problem solving for good versus poor anagram solvers. Quarterly Journal of Experimental Psychology, 61(7), 1098-1120. doi:10.1080/17470210701449936
Öllinger, M., Jones, G., & Knoblich, G. (2008). Investigating the effect of mental set on insight problem solving. Experimental Psychology, 55(4), 269-282. doi:10.1027/1618-3169.55.4.269 Peirce, J. W., Gray, J. R., Simpson, S., MacAskill, M. R., Höchenberger, R., Sogo, H., Kastman, E., & Lindelev, J. (2019). PsychoPy2: experiments in behavior made easy. Behavior Research Methods, 51, 195-203. doi: 10.3758/ S13428-018-01193-V
R Core Team (2019). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. Retrieved from https://www.R-project.org/.
Richardson, J.T.E., & Johnson, P.B. (1980). Models of anagram solution. Bulletin of the Psychonomic Society, 16(4), 247-250. doi:10.3758/BF03329534
Rights, J.D., & Sterba, S.K. (2019). Quantifying explained variance in multilevel models: An integrative framework for defining R-squared measures. Psychological Methods, 24(3), 309-338. doi:10.1037/met0000184
Weisberg, R.W. (1995). Prolegomena to theories of insight in problem solving: A taxonomy of problems. In R. J. Sternberg, & J. E. Davidson (Eds.), The nature of insight (pp. 157-196). Cambridge, MA: MIT Press.
Weisberg, R. W. (2015). Toward an integrated theory of insight in problem solving. Thinking and Reasoning, 21(1), 5-39. doi: 10.1080/13546783.2014.886625
White, H. (1988). Semantic priming of anagram solutions. The American Journal of Psychology, 101(3), 383-399. doi:10.2307/1423086





