Introduction

The social and economic environment in the first decades of the 21^st century is rapidly changing. As an immediate consequence, people have created new habits, preferences and different behaviors in all economic sectors. Moreover, information and communication technologies have made people more aware of political, social and technological changes, and this has lead to an emerging and more demanding type of consumer, worker and citizen. From this point of view, and in order to face this reality of deep transformation and strategic changes, it is understandable that business models require the use of management systems and/or decision-making processes that may improve the organization’s performance. In this regard, as the business environment becomes more competitive and complex and requires greater use of control mechanisms to provide corrections and/or improvement of results, the need to enhance business processes has triggered the development of many theories and methodologies aimed at providing skills and awareness to policy makers. Considering the increasing number and complexity of these theories and methodologies, we do not attempt herein to stress them. Given the diversity of themes, such an attempt would be too ambitious. It is also not an objective of this study to present any type of modeling and/or empirical studies. In fact, based on a review of the literature, this paper aims to target and discuss some of the ideas and/or perceptions related to the conceptual progress made from “classical” OR - Operational Research - to the evolving MCDA - Multiple Criteria Decision Analysis - approach. By highlighting some of the major characteristics of MCDA and adding to the MCDA diffusion, this paper provides theoretical information to support further research and forecast potential developments in the field. In structural terms, and in addition to this introduction and to the conclusion, this paper is divided into six sections: The need for a decision support process', The traditional approach and the optimum paradigm', Soft approach', Basic characteristics of the MCDM approach', Basic characteristics of the MCDA approach', and, Basic concerns of the European school. The presentation sequence reflects the evolution of OR.

1. The need for a decision support process

The way a problem is conceived varies from individual to individual, and may follow different cognitive routes. Thus, the complexity of each problem depends on how the problem is formulated, the circumstances in which it is made, and by whom it is made. According to Ackoff (1978), Keeney (1992) and Cossette (2003), among others, while trying to understand the complexity of a problem and the factors involved in it, a decision maker will eventually incorporate his/her personal values in the solution-finding process. The incorporation of intrinsic values¹ (Keeney (1992, p. 6) defines values as “principles used for evaluation”. According to the author, “we use them to evaluate the actual or potential consequences of action and inaction, of proposed alternatives, and of decisions. […] Ethics, desired traits, characteristics of consequences that matter, guidelines for action, priorities, value tradeoffs, and attitudes toward risk all indicate values”. See also Bana e Costa (1986)) in a decision process in a vague and imprecise way leads often to the exclusion of variables of great importance for the decision process, and, of course, the exclusion of those variables contributes to the inability to offer a conscious and appropriate solution to the problem under discussion. As Keeney (1992, p. 44) argues, “there is a vast discrepancy between the way decision situations are usually examined and the way they should be in order to be consistent with the decision maker’s values and information”. In this way, Turban (1995, p. 9) adds that “in an unstructured problem, human intuition is frequently the basis for decision making. [...] structured processes refer to routine and repetitive problems for which standard solutions exist”. In practice, this lack of awareness regarding the decision maker’s intrinsic values is seen in the way most individuals seek solutions to their problems (i.e., they depart from a presumed “resolution”, even before considering the type and/or nature of the problem). This approach is also highlighted by Bana e Costa et al. (1999, p. 333), who state that, “people are accustomed to take hard decisions without the support of a formal methodology”. Another contribution, as interesting as it is different, is described by Keeney (1996, p. 545) who argues that, “decision makers usually think of decision situations as problems to be solved, not as opportunities to be taken advantage of’. In practice, according to the author, “a decision problem may not be a problem at all but an opportunity”. Therefore, it seems clear that the absence of reflection on a problem and on the context in which it is presented/defined leads, most of the time, the decision maker to lose the objective of his/her problem whereby an improper solution to the problem may be selected. Given this likelihood, it seems logical to accept that the need to “find” decision support processes that assist people to solve their problems has been experienced for a long time² (Turban (1995, p. 6) reinforces this approach in the specific context of business management).

2. The traditional approach and the optimum paradigm

The previously mentioned need for decision support processes gave rise, in 1935, to the concept of Operational Research (OR). Citing Bouyssou (2005, p. 292), “History really begins in 1935 with the Committee for the Scientific Survey of Air Defence (CSSAD) responsible for the development and implement of radar detection”. According to the author, the historical development of the OR field shows that its contribution was of extreme importance not only to support military issues, but also to support non-military activities, particularly in the period between 1945 and 1951. However, as stated by Bouyssou (2005, p. 293), “the history of OR in this period is less well known than that of the heroic times of War”. Based on this evolution, different approaches have emerged (such as: linear, nonlinear, integer and dynamic programming). Those approaches found their peak during the 1960s, and the traditional OR emerged with the objective of bringing a higher degree of rationality to the decision support process (Roy and Vanderpooten, 1997; Checkland, 2001a). In particular, Bouyssou (2005) made it clear that this period was marked by a phase of relative social and economic stability that created the necessary conditions for the development of the exact sciences (e.g., engineering and mathematics), and to the adoption of a position of absolute objectivity in the problem solving processes. For this author, this period was strongly marked by the predominance of the single criterion analysis, which is characterized by the search for an optimal solution supported by normative mathematical models. Therefore, up to the 60s, the OR field was dominated by a paradigm³ (Mingers and Brocklesby (1997, p. 490) define the term paradigm as “a very general set of philosophical assumptions that define the nature of possible research and intervention”. Bouyssou (2005) alerts to the fact that the single criterion approach is subjected to the optimum paradigm, assuming it as a basic axiom used in all research fields) of incessant searching for optimal decisions and that paradigm became the main justification for the development of new methods and approaches. That incessant search for optimum solutions led to the assumption that any other solution would be worse, or at least equivalent, resulting in the disposal of many other good solutions. Roy (1985) sets out three main characteristics of this approach: (1) presence of a clear set of feasible alternatives; (2) a value function f that reflects accurately the preferences of the decision maker; and, (3) a well-formulated mathematical problem. Following this, it seems clear that the main concern of the traditional single criterion approach was to find whether there was a solution that could be in line with the way the problem was formulated, and, therefore, the basic concern of OR was aimed at finding optimum solutions for the problems. Consequently, it is understood that the use of OR in the 60s was limited to the use of optimization techniques, assuming that any activity could be defined as searching systems for the optimums. Checkland (1999) and Rosenhead and Mingers (2001) define it as the hard, orthodox or traditional approach of OR. In line with Rosenhead (2001, p. 184), traditional OR can also be called “rational comprehensive planning”, with the following steps: identification of objectives; identification of alternatives; prediction of the consequences; evaluation of the consequences on a common scale; and, selection of the action that provides the greatest benefit. Accordingly, Rosenhead and Mingers (2001) argue that the characteristics of the hard paradigm are: formulation of the problem around a single goal and in order to achieve an optimum⁴ (If the existence of multiple objectives was recognized, they were converted into a single scale) , the need for a significant amount of data, existence of a previous consensus regardless of a passive attitude from the decision makers, the assumption that a decision is only allowed to obtain direct corrective action, and the attempt to eliminate uncertainty and make decisions on anticipation. Based on this guidance, it can be stated that the researchers of the “classical school” always faced a decision as a scientifically understood act, based on the assumptions of rationality and maximum objectivity⁵ (Quoting Turban (1995, p. 52), “it is assumed that a rational decision maker knows exactly what the goal of making a decision is and how its attainment is going to be measured. It is also assumed that this decision maker knows all the alternatives and their precise relationship to various goal attainment levels. Finally, it is assumed that the decision maker will always prefer an alternative with a high level of goal attainment over an alternative with a lower level of goal attainment”. For a further distinction between rational and satisfactory decisions, see, for instance, Sacco (1996) and Rosenhead and Mingers (2001)) . However, Roy (1985), В ana e Costa (1993b) and Checkland (1999), among others, pointed out the fact that adopting the traditional approach in a decision support system involves adopting a reductionist and deterministic view of reality, inherited from exact sciences and with negative epistemological consequences⁶ (The context of this approach shows that its roots are clearly linked to a mechanistic thinking of science. Thus, the criticisms are based on the positions of several authors, such as Ackoff (1999), Checkland (1999) and Hammond et al. (2002). In particular, Mackenzie et al. (2004, p. 3) state: “restricting the role to mere calculation support is to restrict the help that may be given). In particular, В ana e Costa (1993a, p. 4) argues that “this good faith in scientific cooperation, the belief that any decision problem is at least a solution that, with sufficient resources and time, can be objectively demonstrated as the optimal decision, runs the risk, set out to build [...], biased and inadequate models to real problems that policy makers face”. Indeed, the criticism of these authors seems to suggest that, in making up problems for an optimal solution, people generally tend to think of a single goal, and/or multiple goals reducible to a single one through a scale of compensation. In these situations, decision-making tends to occur without the interaction and participation of all stakeholders. As such, conflicts of interests are supposedly solved by a submission to rational calculation and reference to a single (and most probably autocratic) decision maker. To Rosenhead and Mingers (2001), while OR is guided by a linear sequence such as: models -> techniques -> solutions, we cannot act upon more complex problems, which are characterized by the presence of uncertainty and/or do not have the amount of data required by the orthodox models. Similarly, Turban (1995, p. 45) states that, “because reality is too complex to copy exactly and because much of the complexity is irrelevant to the specific problem [...] if reality differs significantly from the model, optimization cannot be used”. Therefore, it is precisely this critical line that highlighted the main aspects of a new approach to decision-making: the Soft Approach. This line of policy is well explored by Friend (1995, p. 231), who claims that “the eighties saw a growth of interest - especially in Britain - in what became seen as a new class of ‘soft’ OR methods, to be distinguished from those ‘harder’ methods based on more traditional and mathematically rigorous forms of quantitative modeling”.

3. Soft approach: the emergence of a new paradigm

The evolution in the resolution of complex problems, during the end of the 1960s, led to the emergence of new methods to support the decision-making process. Indeed, these new methods were sufficiently relevant to prove that the traditional algorithms were no longer the only tools available to support a decision. Dubois (2003, p. 469) reinforces this interpretation stating: “formal methods are needed to help decision makers make rational choices; but any formal method has its own pitfalls and limitations, and should not be considered as a universal tool applicable to any decision problem”. However, as stated by Mingers and Brock- lesby (1997) and Mingers and Rosenhead (2004), it is important to remember that these new methods do not aim at replacing the traditional procedures. Instead, their existence is based on a complementary logic, considering the undeniable value of orthodox methods, and their efficiency in solving certain types of problems. Despite the complementary logic (and not mutual exclusion), this new current of thought stressed the limited applicability of the most traditional methods and gave place, as a logical consequence, to the development of the so-called soft approaches. According to Checkland (1999) and Rosenhead and Mingers (2001), this new approach adopts a type of “alternative paradigm”, characterized by non-optimal situations, reduced need for data, simplicity and transparency, people as active elements of the decision process, and, conditions that provide bottom-up planning, and acceptance of uncertainty. Table 1 aims to compare the main features between both paradigms (i.e., hard and soft paradigms).

Table 1. Comparison of features between paradigms

From the adoption of the new paradigm emerged the basis of several soft approaches. Among the different proposals that have emerged, the use of multiple criteria in the decision-making process should be higblighted. In broad terms, the idea of building models based on the use of different criteria was considered, at the time, bizarre to say the least, since all classical texts of OR argued that the only way to properly formulate a problem was its definition through a single-objective function that represents the efficiency of the system under study (Checkland, 1999; 2001b). However, this period was marked by the appearance of the first ideas associated with the use of multiple criteria⁷ (According to Roy and Vanderpooten (1997), the creation of the ELECTRE methods in the late 60s has been considered a pioneer attempt to try to find answers to the difficulties inherent in a real decision-making process. For further discussion on the ELECTRE methods, see Bana e Costa (1986), Turban (1995), Simpson (1996) and Belton and Stewart (2002). Also in line with Roy and Vanderpooten (1997), the true forerunner of interactive procedures was the POP method – Progressive Orientation Procedure – which was connected to multi-objective linear programming and had already the two steps of classical interactive procedures: dialogue with decision makers and results computation, with preparation of their recommendations for the next interaction) and to the need to deal with systemic approaches composed of a growing variety of new and conflicting interests (Roy, 1985). Thus, the ideas underpinning the use of multiple criteria began to take place and, over the years, there has been an emergence of more specific and detailed methodologies. As recognized by the editors of the Journal of MultiCriteria Decision Analysis, quoted in Bana e Costa et al. (1997, p. 29), “there are differences, significant differences in the underlying principles, between the various methodologies practised around the world”. For Belton and Stewart (2002), from this evolutionary process two new approaches emerged: MCDM - Multiple Criteria Decision Making and MCDA - Multiple Criteria Decision Analysis (or Aid).

4. Basic characteristics of the MCDM approach

For the MCDM approach, Munda (2003, p. 4) states that its main purpose is to elicit “clear subjective preferences from a mythical decision maker and then a well-structured mathematical decision problem thanks to a more or less sophisticated algorithm”. Indeed, the fundamental idea of this approach is to model a problem considering different dimensions (or criteria), rather than a single criterion as in conventional optimization techniques (Denglet, 2005). In line with Mateu (2002, p. 10), “in MCDM it is supposed that there exists ‘something’ that will allow the decision maker to determine which are the best alternatives”. Thus, there is a need to ensure the rationality and legitimacy of the procedures, regarding the decision axioms. Table 2 presents three main characteristics of this approach (cf. Mateu, 2002; Munda, 2003).

Consideration of something pre-existing to achieve the best solution. Multicriteria preferences and a rationally formulated and structured model. Well-conceived mathematical problem.

In accordance with what has been previously mentioned and with the main features of the MCDM approach, synthesized in Table 2, it can be assumed that this approach is still characterized by a deterministic nature, since it has its scope restricted to the comparative study of the relationship between alternatives for defining optimal solutions. Accordingly, although presenting a concern with multiple objectives, the MCDM approach remains strongly linked to the optimum paradigm (Munda, 2003).

5. Basic characteristics of the MCDA approach

Bana e Costa et al. (1997, p. 30) assert that “in contrast to the more classical OR approaches, the multicriteria decision aid framework facilitates learning about the problem and the alternative courses of action, by enabling people to think about their values and preferences from several points of view”. Therefore, and in line with the authors, the MCDA approach can be seen as a new OR branch regarding the treatment of complex problems. In fact, by recognizing that objectivity has limits and by helping decision makers in shaping and/or transforming their own preferences according to their own values, one of the main objectives of multicriteria methods is the construction of something that does not pre-exist. Keeney (1992, p. 154) seems to strengthen this line of thinking, stating that “values are subjective, but they undeniably are part of decision situations. Not modeling them does not make them go away”. Accordingly, it may be stated that it is precisely the recognition that objectivity has limits that allows to distinguishing the two basic types of multicriteria approaches. In dealing with complex problems, the need to consider subjective aspects becomes usually evident (Figure 1).

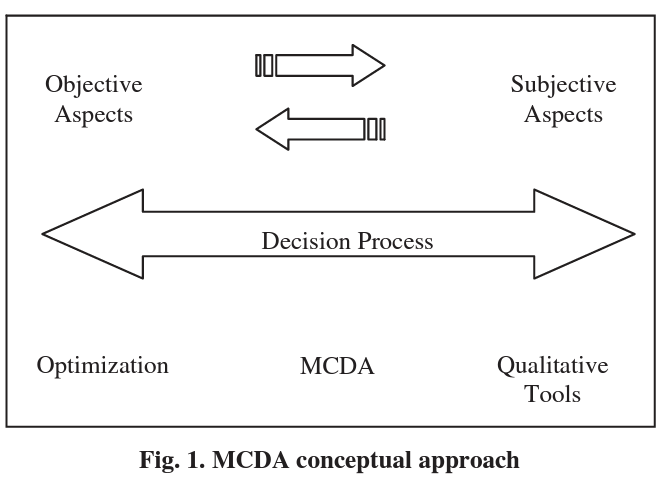
Figure 1 depicts the MCDA conceptual approach and highlights the existing inseparability between decision aspects of an objective and subjective nature. In practical terms, through an interactive and constructive supporting decision process, the MCDA framework aims at providing decision makers with arguments that will enable them to reflect, to shape and/or to validate their own convictions. In doing so, MCDA methods attempt to clarify the decision makers’ thoughts in a given decision-making process and, therefore, MCDA aims at overcoming the assumption that there is a pre-determined model for every problem. In accordance with Bana e Costa et al. (1997, p. 36), “the theory of MCDA is thus an open theoretical field and not a closed mathematical theory solving a specific class of problems”. Roy and Vander- pooten (1997, p. 27) discuss some of the main features that characterize the MCDA approach (Table 3).

The items in Table 3 show that objective factors and options’ characteristics interact with factors of a subjective nature. Thus, it is negligent to omit the importance of subjective factors and/or putting them aside in favor of a purely objective analysis. In fact, the main gap of the single criterion approaches has precisely to do with the non-recognition that objectivity has limits. Even when the existence of multiple objectives is considered, the search for optimization is still emphasized. In accordance with Belton and Stewart (2002, p. 3), “the concept of an optimum does not exist in a multicriteria framework and thus multicriteria analysis cannot be justified within the optimization paradigm frequently adopted in traditional OR [...]. MCDA is an aid to decision-making, a process which seeks to: integrate objective measurement with value judgments; make explicit and manage subjectivity”. Based on a more or less formalized criticism to the single criterion methodologies for not recognizing the limits of a purely objective approach, these authors defend that subjectivity is inherent in all decision-making processes, and a major aim of the MCDA approach is to make individuals’ judgments and preferences explicit, while ensuring transparency in the decisionmaking process. In line with Belton and Stewart (2002, p. 1) “every decision [...] requires the balancing of multiple factors [...] sometimes explicitly, sometimes without conscious thought”. The MCDA approach follows a constructivist approach and recognizes, among other things, the limits of a mathematical optimum. Therefore, there is an MCDA guiding principle that, without any pre-conditions, models are based on the observation of working hypotheses and/or on a set of key elements. These working hypotheses and set of key elements allow decision actors to change the decision-making process in accordance to their own convictions, beliefs and value systems. MCDA is an evolutionary process, which has been associated to the “European School” of OR⁸ (According to Eden (1995) and Dubois (2003), among others, there are two primary schools of multicriteria methodologies: the American School, which defends the most possible descriptive and prescriptive models; and the European School, which adopts a constructivist approach. These approaches serve as behavioral guides throughout the process of the decision support, and have a clear and fundamental influence on the structuring and evaluating phases of the decision-making process). As stated in Roy and Van- derpooten (1997, p. 26), “one of these schools is now commonly referred to as the “European School”, its members being part of a European Working Group [...] which celebrated its 20th anniversary in 1994”.

6. Basic concerns of the European School

According to Roy and Vanderpooten (1997), the main objective of the European School is to create or construct something that, by definition, does not pre-exist. The entity to be built, or created, is seen as a valuable tool to help decision makers to shape and/or to transform their preferences and make decisions on the basis of their objectives. As described in Bana e Costa et al. (1997, p. 29), “in Europe, there has been some tendency to use the terms ‘decision aid’ (or ‘analysis’), instead of ‘decision making’, to emphasize the distinction between the decision maker and the management scientist providing aid or analytical support to the decision making”. Indeed, adopting a constructive way means that the scope is not to describe or to discover, but to create or to build something that allows decision makers to follow their own convictions, objectives and value systems. To better understand the European School’s main concerns, it is necessary to emphasize that in its environment there is no need for pure objectivity awareness. Instead, the presence of subjectivity is required and accepted. This segmentation is also reported by Dubois (2003, p. 470), who states: “roughly speaking there are two groups of approaches: those relying on numerical estimates and aggregation operations, and those based on the use of relations for the modeling and aggregation of preference information. Interestingly, the first group is popular in America, while the other group was basically developed in Europe”. The most striking features of both approaches are outlined in Table 4.

By this logic, Mingers (2000) found that, in recent years, efforts of researchers have been made to obtain concepts, models, axioms, properties and procedures that may be used to produce or extract the information available, and for helping decision makers to clarify their behavior based on good arguments that strengthen or weaken their own convictions. In particular, according to Bana e Costa (1986) and Bana e Costa et al. (1997), diversification showed three major guidelines: (1) Outranking (“Surclassement” in the French literature) that, accepting the incomparability, aims at aggregating the decision maker’s preferences through the construction and use of binary relations⁹ (For Bana e Costa (1986, p. 63), these approaches are based on a “partial comparability axiom”, in which preferences can be shaped by four distinct binary relations, not necessarily transitive: I – Indifference; P – Strict preference; Q – Preferably low and R – Incomparability); (2) Interactive Methods that, based on successive interactions between decision makers and analyst, are focused on a progressively decreasing number of actions and consequences; and, (3) Aggregation Approaches through a Single Criterion of Synthesis, which seek to aggregate the preferences through the construction and use of aggregation functions. With regard to the latter direction, one of the most popular methods is the AHP - Analytic Hierarchy Process¹⁰ (To Turban (1995, p. 212), “the AHP developed by Saaty (1980) helps the decision maker to arrive at the best decision in a case of multiple conflicting objectives (criteria). […] With it, one organizes thought and intuition in a logical fashion using a hierarchy and enters judgments according to understanding and experience. This approach tolerates uncertainty and allows for revision so that individuals and groups can grapple with all their concerns”. Also according to this author, “problems are broken down into smaller constituent parts so the decision maker makes only simple pairwise (two at a time) comparison judgments throughout the hierarchy to arrive at overall priorities for the alternatives of action. The decision problem may involve social, political, and technical factors; several parties; and many objectives, criteria, and alternatives; and may require negotiation”. For further analysis, see Saaty (1980), MacStravic Boucher (1991), Weber (1993), Davies (1994) and Belton and Stewart (2002)) . Based on criticisms of the AHP, other approaches have been designed such as MACBETH by Bana e Costa and Vansnick (1994). In line with Bana e Costa et al. (1997, p. 32), “the path opened by Saaty to the struction of cardinal criteria- functions from absolute semantic judgments concerning well chosen stimuli, is an ingenious and inspiring idea for future research, in spite of certain criticisms of the AHP technique [...] as revealed by the recently developed MACBETH approach ".

Conclusion

This paper has provided an overview of the main evolutionary lines found between traditional OR (based on the so-called optimum paradigm) and the new methodologies of multicriteria decision support - MCDA - based on the so-called soft paradigm. After the analysis of the fundamental principles that guide this activity, special emphasis has been given to the fact that MCDA understands the decision process as complex, and is composed of different actors with different perceptions and value judgments on the problems. Indeed, it was possible to note that this new approach highlights the limits of objectivity, taking into account the subjectivity introduced by the actors, and admitting the possibility that optimal solutions may not exist. By accepting that the inter-relationship between decision actors, the way that information flows, the characteristics of the organization and the leadership style are factors that profoundly affect the decision-making process, the MCDA approach states that the decision-making process is an activity of inherent complexity and, potentially, one of the most controversial. This seems to make clear not only the need to choose between possible alternatives of action, but also between different views and ways of evaluating those alternatives. Therefore, a whole range of factors directly and/or indirectly related to the decision process must be considered and it needs to be accepted that, in the absence of an optimum solution, a commitment solution may be acceptable and/or judged as satisfactory. This is, precisely, the corollary of the MCDA approach.

Acknowledgement

This paper is one of the outcomes of a post-doctoral program undertaken at the Center for Advanced Studies in Economics and Econometrics (CASEE) of the University of Algarve, Portugal (Sept. 2008 / Sept. 2009). The first author is grateful to the University of Algarve for the institutional support.

References

1. Ackoff, R. (1978). The Art of Problem Solving: Accompanied by Ackoff’s Fables, New York: John Wiley & Sons.


2. Ackoff, R. (1999). Ackoff’s Best: His Classic Writings on Management, New York: John Wiley & Sons.


3. Bana e Costa, C. (1986). Apoio ä Tomada de Decisäo Segundo Criterios Multiples, Avaliaqdo de Projectos e De- cisäo Publica, Fascfculo I, AEIST/UTL.


4. Bana e Costa, C. (1993a). Processo de Apoio ä Decisäo: Actores e AcQÖes, Avaliagäo de Projectos e Decisäo Publica, Fascfculo П, AEIST/UTL.


5. Bana e Costa, C. (1993b). Tres Convicföes Fundamentais na Pratica do Apoio ä Decisäo, Lisboa, CESUR/UTL.


6. Bana e Costa, C. and Vansnick, J. (1994). Uma Nova Abordagem ao Problema da Construgao de uma Fungao de Valor Cardinal: MACBETH, Avaliagao de Projectos e Decisäo Publica, Fascfculo VI, AEIST/UTL.


7. Bana e Costa, C., Ensslin, L., Correa, E. and Vansnick, J. (1999). Decision Support Systems in Action: Integrated Application in a Multicriteria Decision Aid Process, European Journal of OR, 113, pp. 315-335.


8. Bana e Costa, C., Stewart, T. and Vansnick, J. (1997). Multicriteria Decision Analysis: Some Thoughts Based on the Tutorial and Discussion Sessions of ESIGMA Meetings, European Journal of OR, 99, pp. 28-37.


9. Belton, V. and Stewart, T. (2002). Multiple Criteria Decision Analysis: An Integrated Approach, Dordrecht: Kluwer Academic Publishers.


10. Boucher, T. and MacStravic, E. (1991). Multiattribute Evaluation within a Present Value Framework and its Relation to the Analytic Hierarchy Process, The Engineering Economist, 37 (1), pp. 1-32.


11. Bouyssou, D. (2005). OR in War and Peace, The British Experience From 1930s to 1970 (Book Review), European Journal of OR, 161, pp. 292-294.


12. Checkland, P. (1999). Systems Thinking, Systems Practice, Chichester: John Wiley & Sons.


13. Checkland, P. (2001a). Soft Systems Methodology, in Rosenhead, J. and J. Mingers (eds.), Rational Analysis for a Problematic World Revisited: Problem Structuring Methods for Complexity, Uncertainty and Conflict, Second Edition, Chichester: John Wiley & Sons, pp. 61-89.


14. Checkland, P. (2001b). Soft Systems Methodology in Action: Participative Creation of an Information Strategy for an Acute Hospital, in Rosenhead, J. and J. Mingers (eds.) Rational Analysis for a Problematic World Revisited: Problem Structuring Methods for Complexity, Uncertainty and Conflict, Second Edition, Chichester: John Wiley & Sons, pp. 91-113.


15. Cossette, P. (2003). Les Cartes Cognitives au Service de L’Etude des Organisations, in Cossette, P. (ed), Cartes Cognitives et Organisations, Les Editions de L’ADREG, online at http://www.editions-adreg.net [18 November 2004], pp. 17-30.


16. Davies, M. (1994). A Multicriteria Decision Model Application for Managing Group Decisions, Journal of the OR Society, 45 (1), pp. 47-58.


17. Dubois, D. (2003). Evaluation and Decision Models: A Critical Perspective (Book Review), Fuzzy Sets and Systems, 139, pp. 469-472.


18. Eden, C. (1995). On Evaluating the Performance of‘Wide-Band” GDSS’s,EuropeanJoumalofOR, 81, pp. 302-311.


19. Friend, J. (1995). Supporting Developmental Decision Processes: The Evaluation of an OR Approach, International Transactions in OR, 2 (3), pp. 225-232.


20. Hammond, J., Keeney, R. and Raiffa, H. (2002). Smart Choices: A Practical Guide to Making Better Life Decisions, New York: Broadway Books.


21. Keeney, R. (1992). Value-Focused Thinking: A Path to Creative Decisionmaking, Harvard: Harvard University Press.


22. Keeney, R. (1996). Value-Focused Thinking: Identifying Decision Opportunities and Creating Alternatives, European Journal of OR, 92, pp. 537-549.


23. Lenglet, R. (2005). Application of Multiple-Criteria Decision Analysis in Open Distributed Processing Systems Management, Tokyo Institute of Technology, online at http://spa.jssst.or.jp/summer-2005/paper/05014.pdf [25 de November 2005].


24. Mackenzie, A., Pidd, M., Rooksby, J., Sommerville, I., Warren, I. and Westcombe, M. (2004). Wisdom, Decision Support and Paradigms of Decision Making, European Journal of OR, online at http://www.sciencedirect.com [18 November 2004].


25. Mateu, A. (2002). ClusDM: A Multiple Criteria Decision Making Method for Heterogeneous Data Set,D. Thesis, Universität Politecnica de Catalunya.


26. Mingers, J. (2000). Variety is the Spice of Life: Combining Soft and Hard OR/MS Methods, International Transactions in OR, 7, pp. 673-691.


27. Mingers, J. and Brocklesby, J. (1997). Multimethodology: Towards a Framework for Mixing Methodologies, Omega: The International Journal of Management Sciences, 25 (5), pp. 489-509.


28. Mingers, J. and Rosenhead, J. (2004). Problem Structuring Methods in Action, European Journal of OR, 152, pp. 530-554.


29. Munda, G. (2003). Multicriteria Assessment, International Society for Ecological Economics, online at http://www.ecoeco.org [25 November 2005].


30. Rosenhead, J. (2001). Robustness Analysis: Keeping Your Options Open, in Rosenhead, J. and J. Mingers (eds.) Rational Analysis for a Problematic World Revisited: Problem Structuring Methods for Complexity, Uncertainty and Conflict, Second Edition, Chichester: John Wiley & Sons, pp. 181-207.


31. Rosenhead, J. and Mingers, J. (2001). A New Paradigma of Analysis, in Rosenhead, J. and J. Mingers (eds.) Rational Analysis for a Problematic World Revisited: Problem Structuring Methods for Complexity, Uncertainty and Conflict, Second Edition, Chichester: John Wiley & Sons, pp. 1-19.


32. Roy, B. (1985). Methodologie Multicritere dAide a la Decision, Paris: Economica.


33. Roy, B. and Vanderpooten, D. (1997). An Overview on “The European School of MCDA: Emergence, Basic Features and Current Works”, European Journal of OR, 99, pp. 26-27.


34. Saaty, T. (1980). The Analytic Hierarchy Process, New York: McGraw-Hill.


35. Sacco, P. (1996). Subjective Metaphysics and Learning From Experience: The Causal Psychology of Rational Choice, Journal of Economic Psychology, 17, pp. 221-244.


36. Simpson, L. (1996). Do Decision Makers Know What They Prefer?: MAVT and ELECTRE П, Journal of the Operation Research Society, 47 (7), pp. 919-929.


37. Turban, E. (1995). Decision Support and Expert Systems: Management Support Systems, 4^th Edition, New Jersey: Prentice Hall Inc.


38. Weber, S. (1993). A Modified Analytic Hierarchy Process for Automated Manufacturing Decisions, Interfaces, 23, pp. 75-84.