ВВЕДЕНИЕ

Обширные эмпирические данные свидетельствуют о том, что темпы экономического роста в различных регионах одной страны существенно различаются. При этом, вероятно, имеет место пространственная корреляция между региональными темпами роста. Россия характеризуется огромной территорией и сильной межрегиональной неоднородностью. Поэтому естественно предположить, что географические факторы оказывают существенное влияние на темпы экономического роста российских регионов. В какой степени различия в темпах роста объясняются сравнительными выгодами географического положения? Является ли относительная близость региона к более развитым соседям экономическим преимуществом? Влияет ли пространственное взаимодействие регионов на темпы экономического роста? Цель статьи - пролить свет на эти вопросы.

Большинство существующих исследований экономического роста российских регионов основано на данных за достаточно короткий период времени (как правило, менее чем 10 лет)¹ (Исключение составляют работы Е.С. Вакуленко [2], Д.А. Зверева и Е.А. Коломак [5], Е.А. Коломак [8]). Используемый в данной статье подход отличается тем, что, во-первых, анализируются данные за достаточно длительный период времени (1996-2012 гг.), во-вторых, учитывается панельная структура данных, в-третьих, в качестве основного индикатора экономической активности используются реальные, а не номинальные среднедушевые доходы.

Существует немало эмпирических исследований, использующих российские данные, в которых тестируется гипотеза о региональной конвергенции [8; 10; 24]² (См. также работы К.П. Глущенко [3; 16], С. Гуриев, Е. Вакуленко [17], где приводятся подробные обзоры исследований конвергенции в российских регионах). Один из основных вопросов, поднимаемых в рамках этой литературы, - роль пространства в экономическом росте регионов. Так, тест Морана использовался для выявления региональных клубов конвергенции в работе Ф. Карлёра [14], сгустков конвергенции регионов по ВРП на душу населения О. Лугового и др. [9]. Важность и актуальность использования методов пространственной эконометрики подчеркивается тем, что учет возможной пространственной автокорреляции доходов приводит к оценкам скорости бета-конвергенции, которые гораздо ниже значений, найденных для межстрановых исследований сходимости экономик К. Холодилиным и др. [20], а также позволяет изучать влияние межрегиональной миграции на экономический рост (Е. Вакуленко [2]).

Наиболее близкой к настоящему исследованию является работа Т. Бучеллато [13], где автор оценивает модели безусловной и условной бета-конвергенции ВРП на душу населения в российских регионах по данным за период 1999— 2004 гг. и сравнивает результаты оценивания с учетом и без учета пространственных взаимодействий. При этом в работе [13] не учтена проблема эндогенности контрольных переменных и рассматривается достаточно короткий период времени. Поэтому естественно ожидать, что оценки скорости сходимости и интенсивности пространственных взаимодействий являются смещенными. В настоящей статье обе эти проблемы приняты во внимание, полученные оценки скорости сходимости (соответственно, интенсивности пространственных взаимодействий) несколько ниже (соответственно, выше), чем в [13].

Также достаточно близкими к данной статье по постановке проблемы и используемым методам исследования являются работы E.Ä. Коломак [5] и Д.А. Зверева [21], в которых тестируются пространственные модели условной конвергенции. В качестве основных экономических индикаторов используются номинальный среднедушевой ВРП и номинальные бюджетные доходы на душу населения за 1995-2007 гг. Авторы получили отрицательные внешние пространственные эффекты динамики развития регионов и приходят к выводу что в межрегиональных взаимодействиях доминируют эффекты конкуренции. Вероятно, такой вывод связан с тем, что номинальные величины доходов не позволяют учесть неоднородность покупательной способности в регионах и «изолировать» эффект пространственной дисперсии цен. Чтобы избежать этой проблемы, мы переходим к реальным доходам населения, используя при дефлировании региональные индексы цен.

Статья организована следующим образом. В начале приводятся предварительные результаты анализа пространственных взаимодействий между российскими регионами. Далее проверяются основные гипотезы исследования, проведен анализ конвергенции регионов по доходам с учетом и без учета возможной пространственной автокорреляции. Показано, что пространственные экстерналии имеют место, однако оценки их интенсивности довольно чувствительны к выбору матрицы расстояний. Последний раздел содержит заключительные замечания.

ПРОСТРАНСТВЕННЫЕ ВЗАИМОДЕЙСТВИЯ РЕГИОНОВ: ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ

Среднедушевые доходы. Изменение неоднородности и разброса региональных среднедушевых доходов населения изучалось многими авторами различными методами, к наиболее простым из них можно отнести наблюдение за динамикой изменения во времени показателей вариации экономического индикатора развития региона (один из подходов для оценки сигма-конвергенции).

Так, в работе Н.В. Зубаревич [6] снижение за последние годы неоднородности ВРП, региональных показателей бедности, безработицы, зарплаты и доходов показано с помощью динамики коэффициента Джини {рис. 1).

В таблице 1 приведены коэффициенты вариации номинальных среднедушевых доходов населения регионов. Как видно из таблицы, в целом наблюдается уменьшение, хотя и незначительное, вариации показателя.

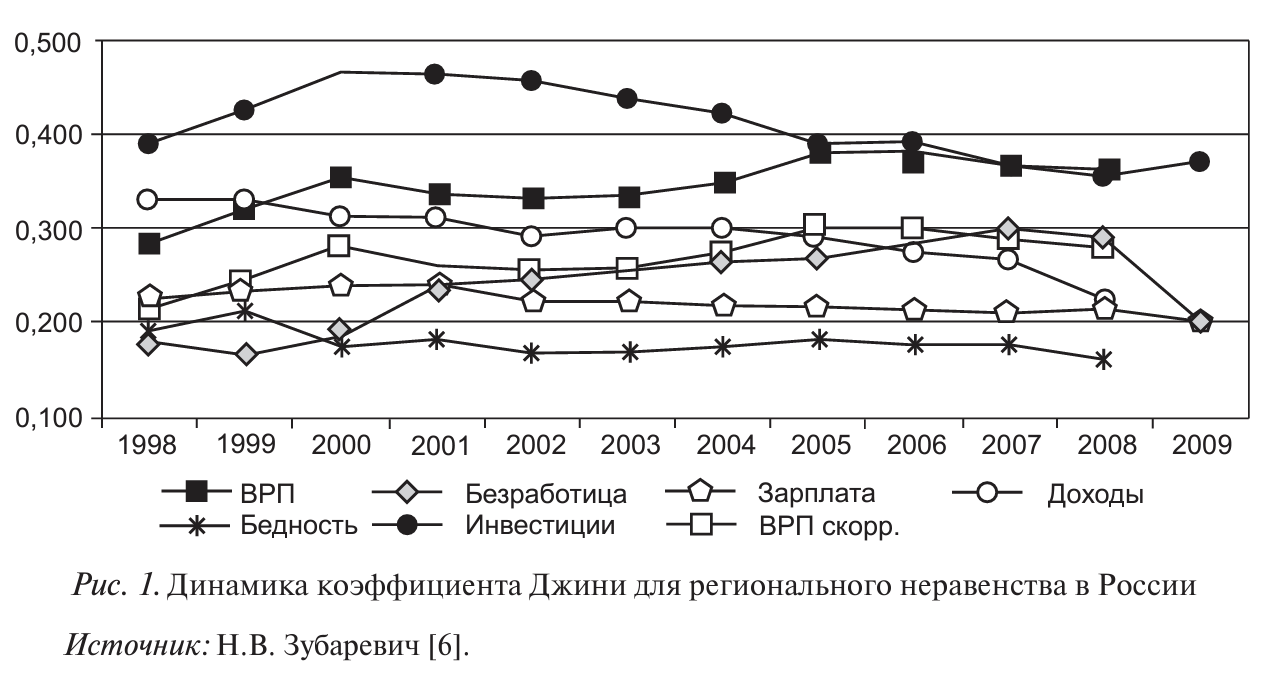
Номинальные величины доходов не учитывают неоднородность покупательной способности, поэтому для возможности пространственного сопоставления следует перейти к реальным доходам населения, дефлированным с учетом региональной специфики.

На рисунке 2 приведена динамика коэффициента вариации реальных среднедушевых доходов населения регионов с 1996 по 2012 г, вычисленного автором по 79 регионам (данные Росстата).

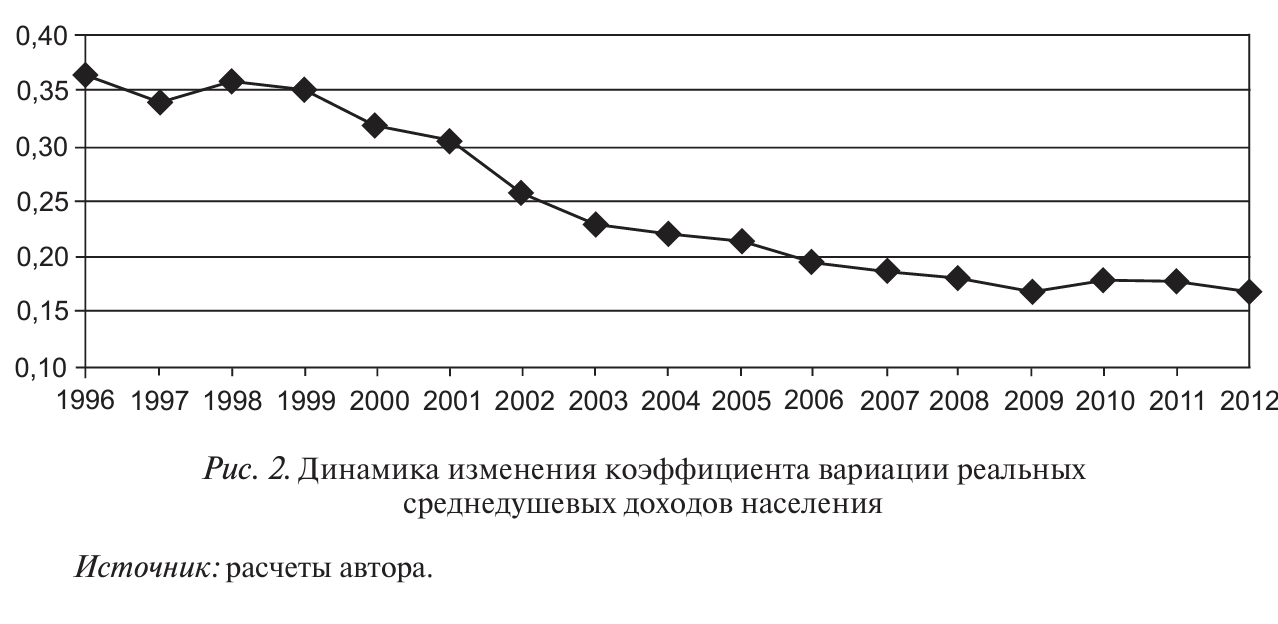
Для приведения номинальных цен к пространственно сопоставимым использовалась стоимость фиксированного набора потребительских товаров и услуг. Стоимость указанного набора доступна с 2002 г., для более ранних дат оценка набора рассчитана с помощью индекса потребительских цен. Как видно из графика, наблюдается тенденция снижения вариации, что подтверждает гипотезу о сигма-конвергенции регионов по доходам населения.

Пространственная автокорреляция среднедушевых доходов. Проверим, объясняется ли распределение региональных среднедушевых доходов регионов пространственным расположением регионов. Для этих целей воспользуемся индексом глобальной пространственной автокорреляции Морана:

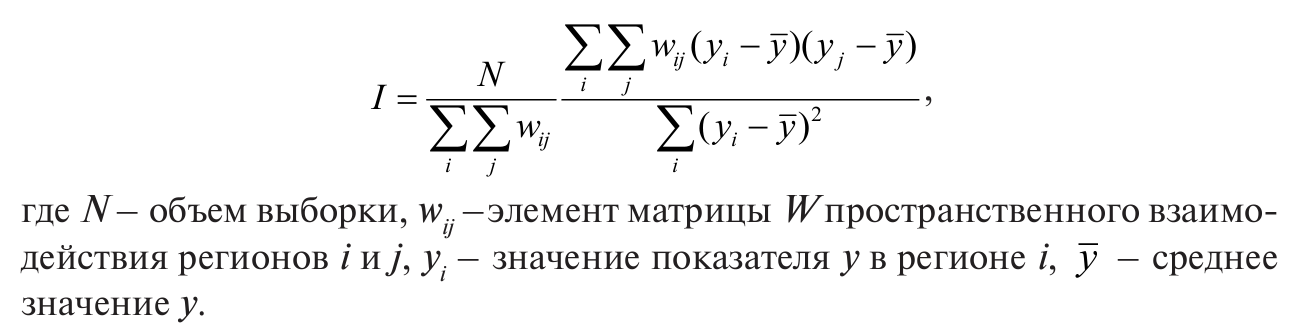
В качестве пространственных весов будем рассматривать следующие матрицы:

• матрица смежности регионов: w_ij = 1, если регионы і и j имеют общую границу (i ≠j), w_ij = 0 в остальных случаях. Матрица смежности была составлена автором по состоянию границ регионов на 2013 г. По регионам, не имеющим сухопутных границ с другими, были приняты следующие допущения: смежными для Сахалинской области регионами указаны Камчатский край и Хабаровский край, с которыми эта область граничит по морю; для Калининградской области пространственным «соседом» указана Псковская область как географически ближайший к ней российский регион;


• модифицированная матрица смежности регионов с поправкой на г. Москву: w_ij = 1, если регионы і или j - г. Москва, w_ij  = 1, если регионы і и j имеют общую границу (i ≠j). w_ij  = 0 в остальных случаях. Указанная модификация пространственной матрицы смежности введена автором в работе [7] для учета специфики российской транспортной сети (столица как крупнейший пересадочный узел);


• матрица обратных географических расстояний между регионами (здесь и далее под расстоянием между регионами понимается расстояние между региональными центрами): w_ij= 1/geodist_ij, где geodist_ij - географическое расстояние между і и j (i ≠j), w_ij = 0.

Расстояние geodist.. рассчитано по географическим координатам как кратчайшее расстояние между городами і и j по поверхности земного шара:

geodist_ij = 6371.arccos (sinLat_isinLat_j + cosLat_icosLat_jcos (Lon_i – Lon_j), где Lon и Lat - соответственно географические долгота и широта, выраженные в десятичных градусах. Поскольку 2 пары регионов (г. Москва и Московская область, г. Санкт-Петербург и Ленинградская область) имеют совпадающие центры, то для расчетных целей координаты городов федерального значения были заданы так, чтобы расстояние до соответствующего областного центра было не нулевым, а равнялось 1 км;

• матрица обратных географических расстояний между регионами с различными значениями порога D отсутствия пространственного взаимодействия: w_ij = 1/geodist_ij , если geodist_ij < D; w_ij = 0, если geodist_ij ≥ D, w_ii = 0. Расчеты проведены для значений порога в 500, 1000 и 2000 км


• матрица обратных кратчайших железнодорожных расстояний, представленная А. Абрамовым [1]: w_ij = 1/d_ij, где d_ij – кратчайшее расстояние между региональными центрами i и j (i ≠j), w_ii = 0

Динамика индексов Морана среднедушевых региональных доходов, рассчитанных по различным матрицам пространственных весов за 1996— 2012 гг, представлена на рисунке 3, все индексы статистически значимы на уровне значимости менее 0,01, они положительны, следовательно, наблюдается пространственно объяснимое распределение регионального экономического индикатора.

Наименьшие значения индекса пространственной автокорреляции среднедушевых доходов соответствуют матрице обратных железнодорожных расстояний. Использование в качестве весов обратных географических расстояний ведет к увеличению индекса Морана. Введение пороговых значений расстояний (500, 1000 и 2000 км) приводит к увеличению показателя тесноты пространственного взаимодействия. Наибольшие значения индекса Морана получены при использовании матрицы смежности регионов, что позволяет сделать вывод о том, что распределение среднедушевых доходов объясняется ближайшими «соседями» региона.

Модифицированная матрица смежности приводит к промежуточному между матрицами смежности и обратных географических расстояний результату, что вполне объяснимо - региональное взаимодействие при добавлении фиктивного «соседа»-столицы в целом ослабевает, здесь сказывается эффект масштаба страны, однако индекс тесноты взаимодействия все же выше, чем для случая железных дорог - недостаточно хорошо развитая железнодорожная сеть не позволяет эффективно использовать географическое положение региона.

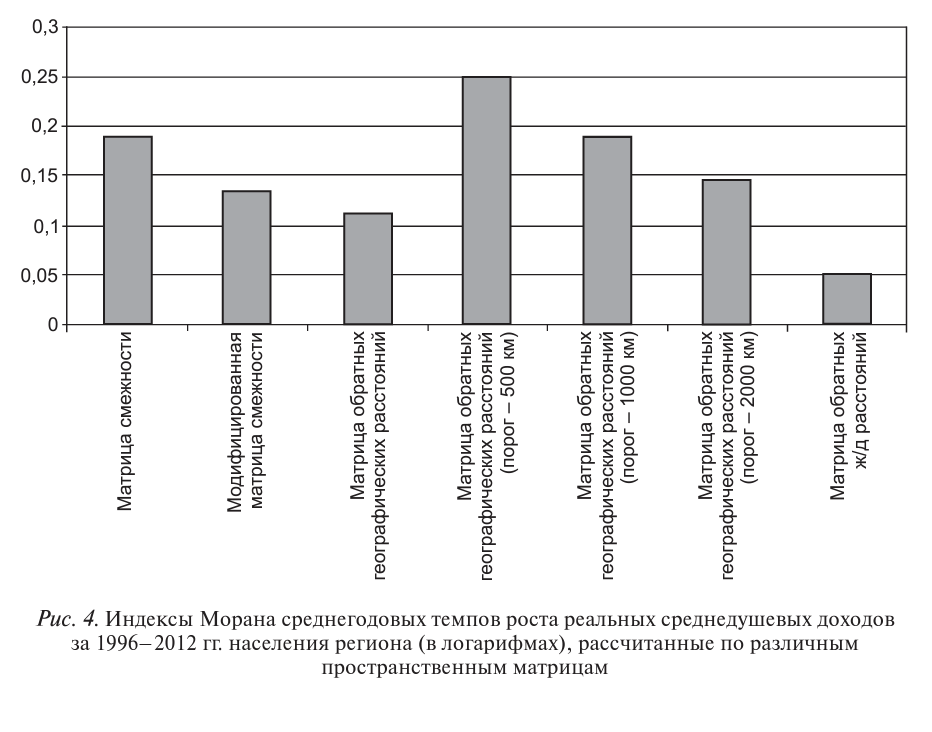
Для логарифмов среднегодовых темпов роста региональных среднедушевых доходов за 1996-2012 гг. также были вычислены индексы Морана (рис. 4), все индексы положительны и статистически значимы на уровне значимости менее 0,01. Наибольшый показатель тесноты пространственного взаимовлияния российских регионов без учета ограничения взаимодействия (с помощью пороговых расстояний) соответствует матрице смежности, 1= 0,189.

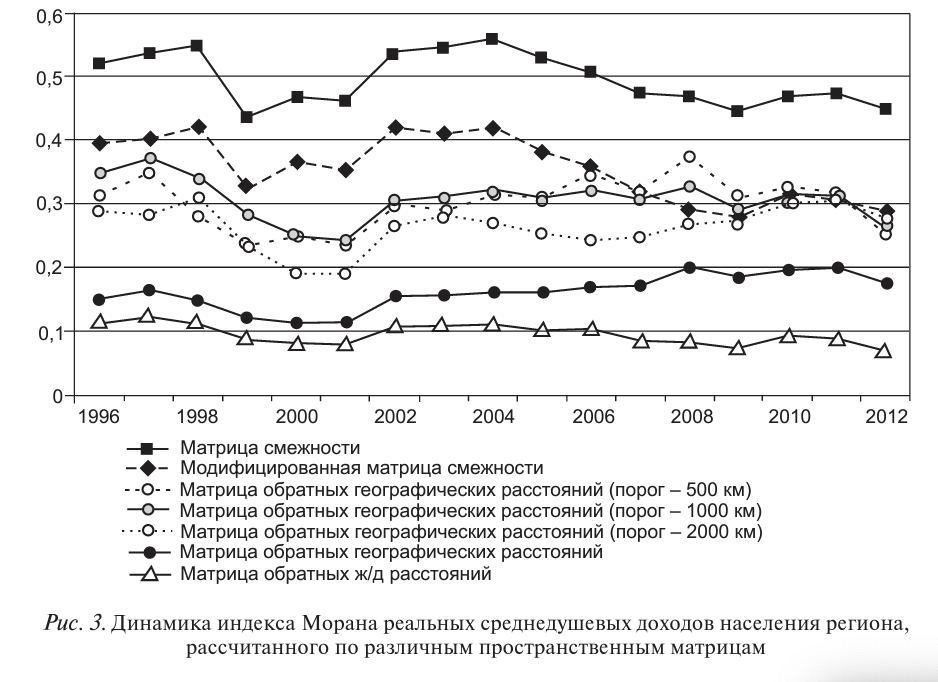
Введение порога пространственного взаимодействия в 500 км приводит к значению индекса Морана 1= 0,243. При величине порога в 1000 км получаем 1= 0,185, что мало отличается от индекса, соответствующего матрице смежности. Возможная интерпретация этого следующая: межрегиональное взаимодействие среднегодовых темпов роста среднедушевых доходов ограничивается неким пороговым значением расстояния (около 1000 км от регионального центра), и пространственное распределение темпов роста среднедушевых доходов носит характер «от соседа к соседу».

Следовательно, основные типы пространственных матриц, которые описывают и объясняют пространственные взаимосвязи российских регионов по исследуемому индикатору и темпам его роста, среди рассмотренных выше, - матрица смежности и матрица обратных географических расстояний с порогом в 1000 км. Необходимо отметить, что пространственное взаимовлияние, описываемое всеми рассмотренными структурами пространственных матриц, положительно и статистически значимо.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ

В работе В. Баумоля [12] исследован экономический рост стран по выборке, охватывающей 1870-1979 гг. по различным экономическим индикаторам, и показано, что страны с низкими начальными показателями демонстрируют более высокие темпы роста, чем изначально богатые страны, в частности, США. Р. Барро и К. Сала-и-Мартин [11] из неоклассической модели роста получили уравнение, ставшее известным как регрессия Барро, связывающее долгосрочные темпы роста экономик с начальными уровнями их среднедушевых доходов. Следует отметить, что более быстрый рост экономик с низкими начальными доходами (бета-конвергенция) необязательно приводит к сокращению неравенства по доходам [4].

Регрессии Барро. Для проверки гипотезы о региональной бета-конвер- генции оценивается регрессия Барро:

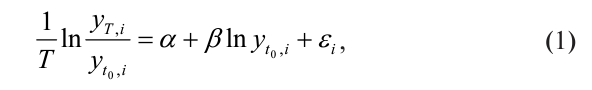
где y_t0,i – реальный среднедушевой доход в регионе i в начальный год (t₀ = 1996), y_t,i - реальный среднедушевой доход в регионе i в последний рассматриваемый год

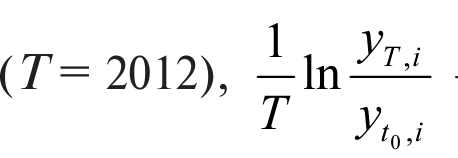
среднегодовые темпы роста реальных среднедушевых доходов, в логарифмах. Если ß отрицательно и статистически значимо, то говорят, что имеет место бета-конвергенция.

На рисунке 5 представлено поле корреляции 78 регионов по начальному уровню среднедушевых доходов населения, соответствующих 1996 г, и среднегодовым темпам роста с 1996 по 2012 г.

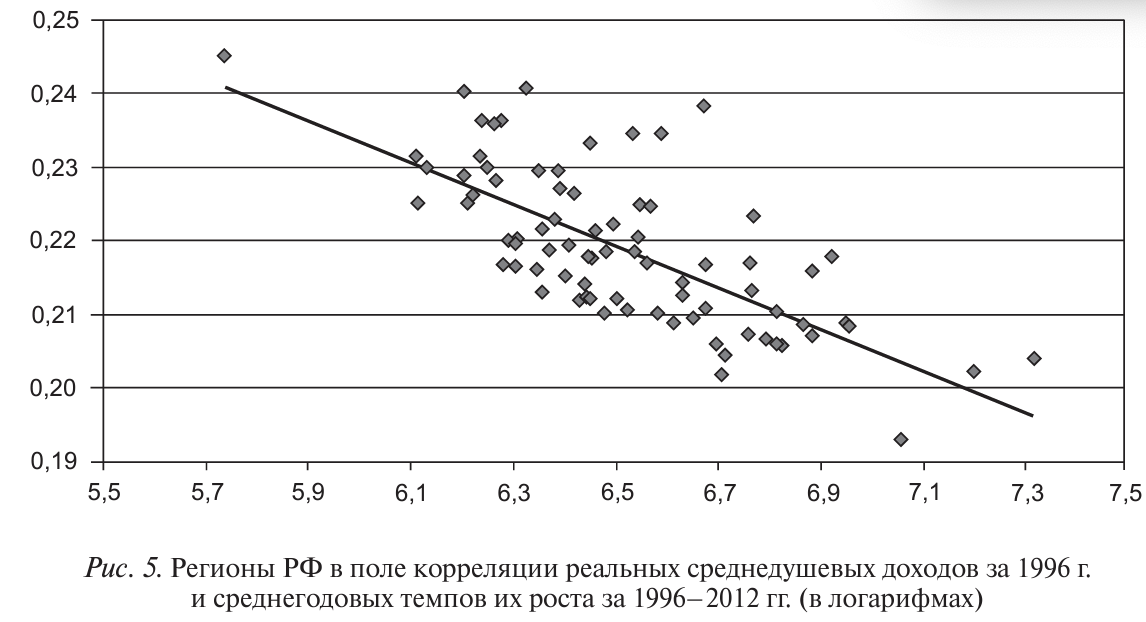
Линия тренда, представленная на рисунке 5, описывается уравнением (1) со следующими оценками коэффициентов:

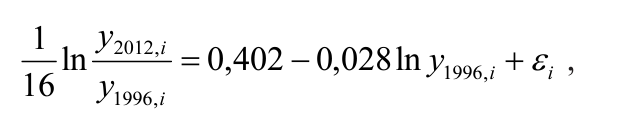
полученными методом наименьших квадратов (МНК), коэффициент детерминации R² = 0,503, значение F-статистики Фишера 77,785 соответствует уровню значимости 2,671Е-13. Следовательно, нет оснований отклонять гипотезу об абсолютной бета-конвергенции российских регионов по среднедушевому доходу.

Рассматриваемый временной интервал равен 16 годам, это не столь длительный срок для выводов по регрессии Барро, оцененной на кросссекционных данных. Поэтому следует учесть возможные вариации региональных среднедушевых доходов в рассматриваемый временной период и получить оценки коэффициентов уравнения конвергенции по панельным данным:

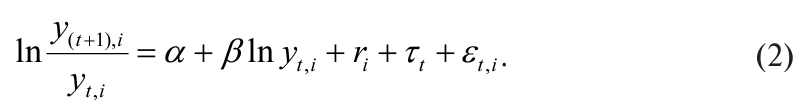
Чтобы элиминировать региональные различия, в уравнение (2) вводятся индивидуальные фиксированные эффекты регионов, постоянные во времени: г, которые описывают влияние неучтенных в уравнении факторов на рост среднедушевых доходов. Также учитываются фиксированные эффекты годов: т_t, которые вводятся с помощью набора фиктивных переменных для рассматриваемых лет. Результаты оценивания, полученные МНК, приведены в таблице 2.

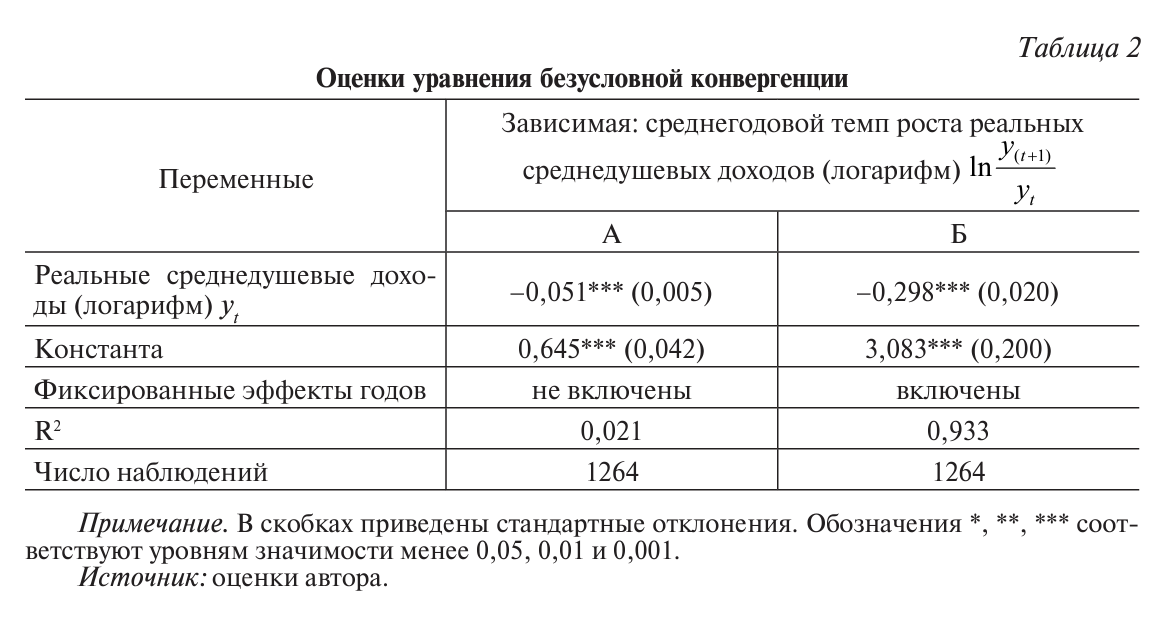
Коэффициент при логарифме среднедушевых доходов отрицателен и статистически значим в обоих столбцах таблицы 1, следовательно, наблюдается бета-конвергенция российских регионов по среднедушевым доходам. Фиксированные эффекты годов статистически значимы на уровне значимости менее 0,001, и их включение в уравнение регрессии существенно повышает величину коэффициента детерминации R², что подтверждает необходимость учета временной вариации индикатора экономического роста в регионах России.

Имеет ли значение пространство? Влияет ли взаимное географическое расположение субъектов РФ на региональную конвергенцию? Этот вопрос неоднократно поднимался исследователями в эмпирических работах. Так, в работе Л. Соланко [24] роль пространства тестировалась включением в уравнение условной конвергенции переменной, показывающей удаленность регионального центра от г. Москвы, но этот показатель не являлся статистически значимым.

В исследовании Д.В. Зверева и ЕА.Коломак [5] в качестве пространственных весов использовались обратные кратчайшие расстояния между региональными центрами по существующим автодорожным сообщениям, в работе О. Лугового и др. [9] - минимальное время в пути, затрачиваемое на преодоление расстояния между региональными центрами по автомобильным дорогам. Экзогенность пространстве иных весов, природа которых зависит не только от географического пространства, но и от доступности транспортных систем, не является бесспорной, поэтому в данной работе используются пространственные веса, сконструированные таким образом, чтобы они зависели лишь от географических координат региональных центров, либо отражали взаимное географическое расположение территорий регионов³ (Единственная из используемых в данной работе матриц пространственных весов, которая не удовлетворяет указанному требованию, – матрица обратных железнодорожных расстояний. Однако экзогенность этой матрицы не вызывает сомнений и объясняется тем, что на сегодняшний день в стране не ведется интенсивного строительства железных дорог).

Размер рынка. Начиная с П. Ромера [23] в теоретических моделях эндогенного роста предполагается, что долгосрочные темпы роста положительно связаны с размером рынка. Это предположение проверялось в работе Л. Джонса [18] на временных рядах по США, однако не подтвердилось.

В российских исследованиях эффект агломерации проверялся в работе О. Лугового [9] на основе данных по 77 регионам за 1997-2004 гг. В качестве основной агломерационной переменной рассматривалась численность населения в главном городе региона. Включение численности населения в уравнение условной конвергенции показывало статистически значимый положительный эффект на темпы роста среднедушевого ВРП.

В данной работе будет проверяться гипотеза о влиянии размера рынка региона на темпы роста среднедушевых доходов.

Спецификация пространственной модели конвергенции регионов. Составим модель условной конвергенции, содержащую пространстве иную компоненту, учитывающую взаимное расположение регионов, а также в качестве объясняющей переменной - размер рынка региона. Размер рынка региона будет рассматриваться как население региона.

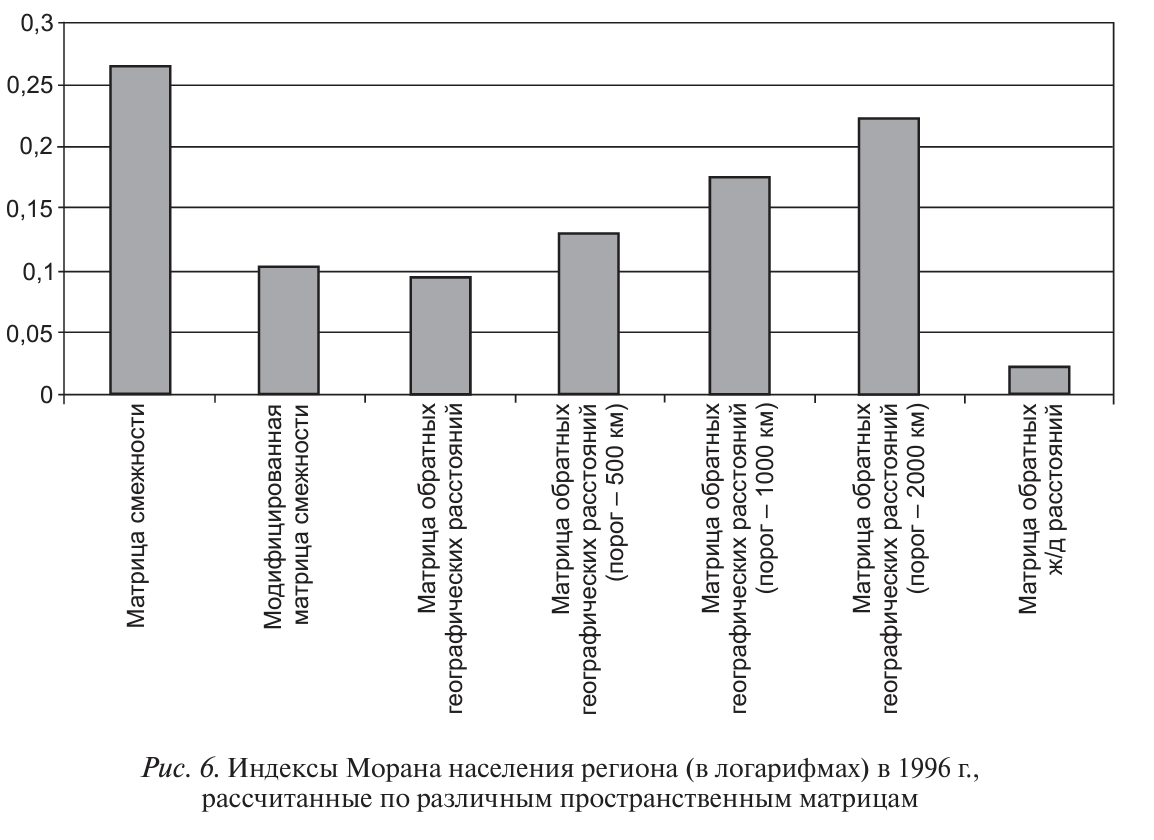
Индекс пространственной автокорреляции населения региона (в логарифмах) для различных пространственных матриц представлен на рисунке 6. В отличие от индекса Морана для среднедушевых доходов (рис. 3) и темпов их роста (рис. 4), пространственное распределение населения по территории страны в наибольшей степени объясняется связями матрицы смежности.

Введем в рассмотрение пространстве иную авторегрессионную модель с авторегрессионными остатками:

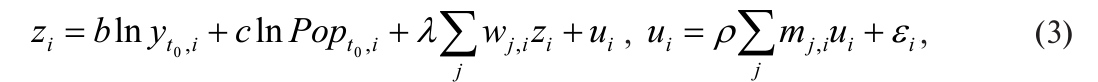
Применение обычного МНК для оценки (3) невозможно, т. к. ввиду наличия эндогенных слагаемых (пространстве иных лагов) в правых частях модели это может привести к смешенным оценкам.

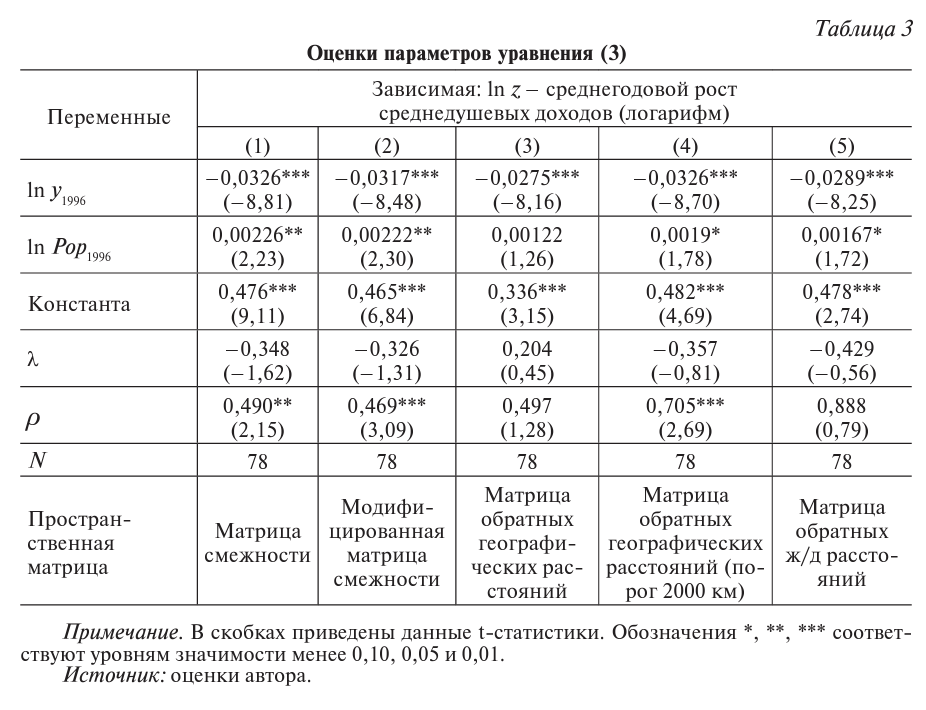
В таблице 3 приведены оценки уравнения (3), полученные обобшенным пространственным двухшаговым МНК (0П2МНК) [19] для различных пространственных матриц. Суть метода заключается в том, что при оценивании используются инструменты, являющиеся пространственно взвешенными исходными переменными, сконструированными с помощью входящих в модель пространственных матриц и их степеней.

В уравнении (3) логарифм населения региона ln Pop₁₉₉₆ является эндогенным показателем, поэтому непосредственное оценивание параметров регрессии (3) дает смещенные оценки. Существуют различные подходы к оцениванию параметров регрессии с эндогенной переменной, в том числе - применение метода инструментальных переменных. В качестве инструмента для In Рор₁₉₉₆ используются датированные значения населения региона ln Pop₁₉₉₆, соответствующие данным переписи населения в Российской империи в 1897 г. Этот инструмент не имеет прямого влияния на темпы роста среднедушевых доходов с 1996 по 2012 г, т. е. является некоррелированным с ошибкой модели. В то же время инструмент коррелирован с объясняющей переменной: коэффициент корреляции соrr[Рор₁₈₉₇; Рор₁₉₉₆) = 0,672, т. е. объясняет вариацию населения региона на 45% (R² = 0,672² = 0,451584)¹.

Распределение населения региона по территории страны объясняется не только начальными демографическими показателями. В случае больших территорий необходимо принимать во внимание пространстве иные различия, в частности, различия в климатических условиях регионов. В региональных
исследованиях в качестве переменных, отражающих климат, используют различные показатели: средняя температура в январе, средняя температура в июле, среднегодовая температура, продолжительность отопительного сезона и др. Например, для учета характера распределения населения по изотермическим территориям в работе Т. Михайловой [22] введен индекс температуры на душу населения.

Поскольку климат и географические условия в каждом регионе уникальны и полностью объясняются географическим положением в пространстве, то для учета специфики региона в регрессии (3) необходимо принять во внимание его местоположение. Поэтому для инструментирования размера рынка наряду с историческими данными использованы географические координаты столиц регионов: географическая широта Lat и географическая долгота Lon (в логарифмах), а также их квадраты. Результаты оценивания множественной линейной регрессии логарифма населения региона в 1996 г. на перечисленные регрессоры приведены в таблице 4, все входные переменные в которой статистически значимы.

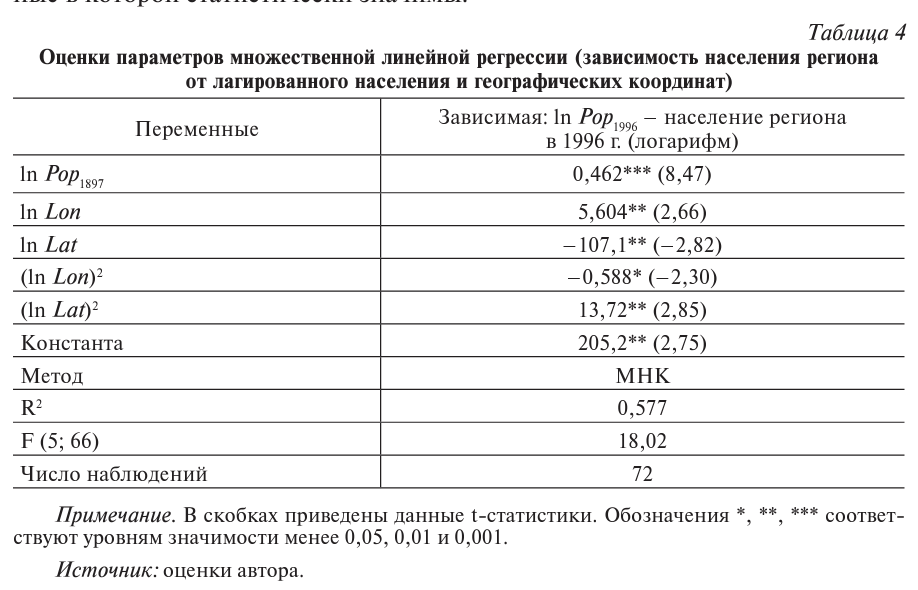
В качестве пространственных матриц в модели (3) были использованы те же самые матрицы, по которым вычислялись индексы Морана на рисунках 4 и 5, кроме обратных географических расстояний с величинами порога в 500 и 1000 км, т. к. эти матрицы в случае 72 наблюдений, соответствующих 1897 г., являются несвязными, что не позволяет применять их в регрессионном анализе. Оценки модели (3) методом ОП2МНК приведены в таблице 5. Согласно полученным оценкам, размер рынка региона является статистически значимым показателем, объясняющим бета-конвергенцию регионов по среднедушевому доходу, причем влияние размера рынка на темпы роста положительно.

Сравнивая оценки коэффициентов при переменной In Рор₁₉₉₆ в таблицах 3 и 4, можно сделать вывод о том, что эндогенность переменной In Рор₁₉₉₆ при оценивании уравнения (3) без использования переменных, выражающих пространственное распределение городов по территории страны, и ретроспективных данных о населении, занижает истинную оценку параметров, соответствующих размеру региона.

Резюмируя, можно утверждать, что размер рынка оказывает положительное влияние на экономический рост. По-видимому, это можно объяснить тем, что наличие у фирм доступа к более широким рынкам стимулирует деловую активность, способствует повышению производительности и, как следствие, ускоряет экономический рост. Такое объяснение согласуется с выводами «новой экономической географии» [15].

Необходимо отметить, что пространственные параметры λ и Ρ во всех случаях, когда они статистически значимы на уровне 0,1 и менее, являются положительными, что подтверждает гипотезу о наличии пространственных компонент взаимовлияния регионов, объясняющих бета-конвергенцию регионов по среднедушевым доходам за рассматриваемый период. Важно подчеркнуть, что рассматриваемые пространственные матрицы недостаточно полно объясняют взаимодействие регионов в смысле статистической значимости оценок пространственных параметров модели (3), причиной чему в частности, может служить использование совпадающих пространстве иных весов весов w_j,i = m_j,i

ЗАКЛЮЧЕНИЕ

Статья посвящена измерению влияния пространственных эффектов на сходимость российских регионов по среднедушевому доходу Проанализирована динамика изменения показателей вариации регионального среднедушевого дохода, отмечено уменьшение неоднородности. С помощью аппарата пространственной эконометрики получены эмпирические подтверждения гипотезы о бета-конвергенции регионов, установлено существенное влияние пространственных особенностей регионов на характеристики конвергенции. При этом установлено, что количественные оценки этого влияния весьма чувствительны к выбору способа выражения пространственного взаимодействия между регионами. Поэтому разработка подхода к обоснованию выбора матрицы пространственных весов представляется перспективным направлением дальнейшей работы.

Кроме того, показано, что размер рынка региона оказывает положительный эффект на региональный экономический рост, то есть имеют место экстерналии масштаба. В качестве основного индикатора размера рынка использовалось население региона, при этом существенное внимание было уделено решению проблемы эндогенности. Проверка робастности полученных результатов путем использования альтернативных мер емкости рынка также является одним из важных направлений дальнейшего исследования.

СПИСОК ЛИТЕРАТУРЫ

1. Абрамов А. Матрица кратчайших расстояний между административными центрами российских регионов. Новосибирск: НГУ, 2000. URL: http://pub.econom.nsu.ru/staff/chair_et/gluschenko/Research/Data/Distances.xls (дата обращения: октябрь 2013).


2. Вакуленко Е.С. Ведет ли миграция населения к межрегиональной конвергенции в России? // Вестник НГУЭУ. 2013. № 4. С. 239–264.


3. Глущенко К.П. Исследование неравенства по доходам между российскими регионами // Регион: экономика и социология. 2010. № 4. С. 88–119.


4. Глущенко К.П. Мифы о бета-конвергенции // Журнал Новой экономической ассоциации. 2012. № 4 (16). С. 26–44.


5. Зверев Д.В., Коломак Е.А. Субфедеральная фискальная политика в России: межрегиональные различия и связи. Серия «Научные доклады: независимый экономический анализ». № 214. М.: Московский общественный научный фонд; Сибирский центр прикладных экономических исследований, 2010. 160 с.


6. Зубаревич Н.В. Регионы России: неравенство, кризис, модернизация. М.: Независимый институт социальной политики, 2010. 160 с.


7. Иванова В.И. О динамике пространственного взаимодействия российских регионов // Экономика и география / науч. ред. А.П. Заостровцев, Л.Э. Лимонов. СПб.: Международный центр социально-экономических исследований «Леонтьевский центр», 2013. С. 96–102.


8. Коломак Е.А. Межрегиональное неравенство в России: экономический и социальный аспекты // Пространственная экономика. 2010. № 1. С. 26–35.


9. Луговой О., Дашкеев В., Мазаев И. и др. Экономико-географические и институциональные аспекты экономического роста в регионах / Консорциум по вопр. приклад. экон. исслед., Канадское агентство по междунар. развитию. М.: ИЭПП, 2007. 164 с.


10. Ahrend R. Speed of Reform, Initial Conditions or Political Orientation? Explaining Russian Regions’ Economic Performance // Post-Communist Economies. 2005. Vol. 17. Issue 3. Pр. 289–317. DOI: 10.1080/14631370500204198


11. Barro R.J., Sala-i-Martin X. Regional Growth and Migration: A Japan – United States Comparision // Journal of Japanese and International Economies. 1992. Vol. 6. Issue 4. Pр. 312–346. DOI: 10.1016/0889-1583(92)90002-L


12. Baumol W.J. Productivity Growth, Convergence, and Welfare: What the Long-Run Data Show, American Economic Review, American Economic Association, 1986. Vol. 76 (5). Pp. 107–285.


13. Buccellato T. Convergence Across Russian Regions: A Spatial Econometrics Approach / Centre for the Study of Economic and Social Change in Europe, SSEES, UCL. Economics Working Papers. No. 72. London, UK. 2007. URL: http://discovery.ucl.ac.uk/17480/1/17480.pdf (дата обращения: 03.10.2014).


14. Carluer F. Dynamics of Russian Regional Clubs: The Time of Divergence // Regional Studies. 2005. Vol. 39. Issue 6. Pр. 713–726. DOI: 10.1080/00343400500213564


15. Fujita M., Thisse J.-F. Economics of Agglomeration: Cities, Industrial Location, and Globalization. 2nd Edition. Cambridge: Cambridge University Press, 2013. 528 p.


16. Gluschenko K. Methodologies of Analyzing Inter-Regional Income Inequality and Their Applications to Russia. William Davidson Institute Working Paper. No. 984. 2010. URL: http://wdi.umich.edu/files/publications/workingpapers/wp984.pdf (дата обращения: 22.09.2014).


17. Guriev S., Vakulenko E. Convergence between Russian Regions / Center for Economic and Financial Research (CEFIR). Working Papers No. 180. 2012. URL: http://www.hse.ru/pubs/lib/data/access/ram/ticket/96/1414379987e18d3914e09bd541074b790e09ac1509/WP180.pdf (дата обращения: 05.09.2014).


18. Jones L., Manuelli R., Stacchetti E. Technology and Policy Shocks in Models of Endogenous Growth / Federal Reserve Bank of Minneapolis. Working Paper. No. 281. 2000.


19. Kelejian H., Prucha I. A Generalized Spatial Two-Stage Least Squares Procedure for Estimating a Spatial Autoregressive Model with Autoregressive Disturbances // Journal of Real Estate Finance and Economics. 1998. Vol. 17. Issue 1. Pр. 99–121. DOI: 10.1023/A:1007707430416


20. Kholodilin K.A., Oshchepkov A., Siliverstov B. The Russian Regional Convergence Process: Where Does it Go? / Berlin. Deutsches Institut fur Wirtschaftsforschung. Discussion Paper. No. 861. 2009. URL: http://www.diw.de/documents/publikationen/73/diw_01.c.95019.de/dp861.pdf (дата обращения: 25.09.2014).


21. Kolomak E.A. Spatial Externalities as a Source of Economic Growth // Regional Research of Russia. 2011. Vol. 1. Issue 2. Pp. 114–119. DOI: 10.1134/S2079970511020080


22. Mikhailova T. Essays on Russian Economic Geography: Measuring Spatial Inefficiency / The Pennsylvania State University. Thesis in Economics. 2004.


23. Romer P. Endogenous Technological Change // Journal of Political Economy. 1990. Vol. 98. No. 5. Pp. 71–102. URL: http://www.jstor.org/stable/2937632 (дата обращения: 20.08.2014).


24. Solanko L. An Empirical Note on Growth and Convergence Across Russian Regions / BOFIT. Discussion Papers. No. 9. 2003. URL: http://www.suomenpankki.fi/pdf/109440.pdf (дата обращения: 09.10.2014).