Эффект Н.А. Бернштейна в оценке параметров тремора при различных акустических воздействиях


Published: Dec. 31, 2015
Latest article update: Dec. 19, 2022
Abstract
С использованием специальных методов (теории хаоса-самоорганизации) и методов традиционной статистики изучалась реакция регуляторных систем нервно-мышечной системы человека на различные акустические воздействия (белый шум, ритмическая музыка, классическая музыка, хард-рок). Исследовалось состояние слухового аппарата человека при акустическом воздействии на него и без воздействия, при этом использовался подход, основанный на анализе параметров квазиаттракторов параметров нервно-мышечной системы (постуральный тремор) при одновременной регистрации треморограмм левой и правой рук испытуемых (в условиях звукового воздействия). Акустическое воздействие играло роль возмущающего фактора для системы регуляции тремора (и мышечной активности), оно изменялся психофизиологическое состояние испытуемого (системы С и Д регуляции по Н.А. Бернштейну). Разработанный метод матричного анализа обеспечивает идентификацию систем с хаотической организацией, которая была продемонстированна в настоящей работе на примере сравнения треморограмм левой и правой рук испытуемых при различных акустических воздействиях.
В работе акустические воздействия рассматриваются как возмущающие воздействия, влияющие на состояние психического гомеостаза. При этом главная задача – это количественная оценка психического состояния испытуемых посредством расчётов параметров треморограмм. Предлагается метод расчёта параметров квазиаттракторов, который демонстрирует различия в треморограммах левой и правой руки и в реакциях тремора на акустические воздействия. Этим, фактически, предлагается новый подход в оценке моторной асимметрии и метод регистрации параметров психического гомеостаза по хаотической динамике треморограмм. Задача регистрации психического статуса человека в когнитивной психологии решена с большой долей неопределённости (Н.А. Бернштейн).
В работе акустические воздействия рассматриваются как возмущающиеся воздействия, влияющие на состояние психического гомеостаза. При этом главная задача – это количественная оценка психического состояния испытуемого посредством расчетов параметров треморограмм. Предлагается метод расчета параметров квазиаттракторов, который демонстрирует различия в треморограммах левой и правой руки и в реакциях тремора на акустические воздействия. Фактически предлагается новый подход в оценке и моторной асимметрии, и метод регистрации параметров психического гомеостаза по хаотической динамики треморограмм.
Keywords
Энтропия Шеннона, психофизиологическое состояние, акустическое воздействие, нервно-мышечная система человека
Около 70 лет назад Н.А. Бернштейн выявил эффект «повторения без повторений» (Бернштейн, 2004) при изучении различных движений человека. Однако до настоящего времени проблема количественного описания характера и роли субкортикальных уровней в организации движений остается открытой. Любые сложные психофизиологические динамические системы (ПФДС) в виде систем регуляции (организации) движений являются уникальными и невоспроизводимыми точно системами. Именно это пытался сказать Н.А. Бернштейн, характеризуя четыре уровня построения движения. Для исследования таких сложных систем уже недостаточны традиционные методы, применяемые в детерминистском и стохастическом подходах (ДСП), где мы имеем полную определенность начального состояния системы и необязательно полную (в частности, в стохастике) для конечного состояния (Адайкин, 2008; Ануфриев, 2008; Аушева, 2008; Бернштейн, 2004; Брагинский, 2006, 2010). Определённость начального состояния x(t0) любого вектора психофизиологического состояния испытуемого в ДСП является обязательным условием. Обязательным условием ДСП является и неоднократное воспроизведение начального состояния системы в момент времени t0, и наличие возможности стационарных режимов и точек покоя, которые в рамках ДСП представляются математически как dx/dt=0, где x=x(t)=(x1,…, xm)T – вектор состояния ПФДС, здесь t-текущее время, dx/dt – производная координаты x.
С точки зрения детерминистского подхода, многократное повторение процесса обеспечивает идентификацию модели ПФДС в фазовом пространстве состояний (ФПС), а в стохастике – статистической функции распределения f(x). Именно такой подход мы сейчас и используем в анализе повторяемости треморограмм (ТМГ) испытуемых. Стохастика всегда требует повторения процесса, в котором его конечный результат будет флуктуировать около среднего значения <х>. В этом случае мы всегда имеем неравномерное распределение случайной величины x(t) в отличие от теории хаоса и самоорганизации (ТХС), где обычно имеются особые хаотические изменения распределения значений параметров xi всего вектора состояния системы (ВСС), как любой сложной системы в фазовом пространстве состояний (Брагинский, 2006; Буров, 2010; Ведясова, 2012; Вохмина, 2014; Гавриленко, 2013; Добрынина, 2015; Еськов, 2009). Наличие dx/dt=0 или сохранение статистических функций распределения f(x) в ДСП является необходимым условием стационарности x(t), т.е. любых ПФДС. В наших исследованиях обычно x1(t) представляет положение конечности (пальца) по отношению к датчику регистрации тремора, а x2=dx1/dt – скорость изменения этой координаты x1(t).
Одним из наиболее распространенных неблагоприятных физических факторов в условиях производства или в быту является шумовое воздействие. Любые звуковые воздействия способны существенно повлиять на параметры ПФДС человека. Поэтому можно рассматривать изменения параметров нервномышечной системы (НМС) человека в виде характеристик (треморограмм) левой и правой рук испытуемых при различных видах звукового воздействия (Вохмина, 2014; Гавриленко, 2013; Добрынина, 2015; Еськов, 2009, 2010; 2014а, 2014б, 2015) как реализацию НМС на звуковые воздействия. Использование традиционных статистических методов расчета f(x), спектральных плотностей сигнала (СПС) – треморограмм (ТМГ) и их автокорреляционных функций A(t), как мы сейчас доказываем, не является эффективным подход в изучении ПФДС.
Для всех живых организмов акустическое воздействие является одним из важнейших факторов окружающей среды. Согласно современным представлениям, музыка разных направлений, благодаря ритму и звуку, способна оказывать неоднозначное влияние на все живые организмы, в том числе, и на человека. Очевидно, что в рамках представлений Н.А. Бернштейна о системах регуляции движений на субкортикальном уровне (системы С и Д) мы должны иметь возможность регистрации изменений и самих треморограмм (при внешних акустических воздействиях). Однако ДСП показывает полное отсутствие возможностей описания тремора из-за хаотической динамки выборок ТМГ. Этот факт и лег в основу настоящей работы (Еськов, 2014б, 2015; Козлова, 2010; Филатов, 2010, 2012, 2014).
Управление основными движениями тела человека и его сенсорными функциями равномерно распределено между двумя полушариями мозга. Однако физическая (морфологическая) симметрия мозга не означает, что правая и левая стороны равноценны во всех отношениях. В связи с этим, изучение функциональной асимметрии мозга – важная проблема физиологии человека и психофизиологии, т.к. участие высшей нервной деятельности человека обеспечивает хаос в ПФДС, который, однако, тоже функционально ассиметричен.
Объект и методы исследования
Эксперимент включал в себя 5 этапов исследования. На первом этапе у испытуемых регистрировались параметры постурального тремора в виде координаты пальца по отношению к датчику х1=х1(t) в спокойном состоянии (при отсутствии активного акустического воздействия). На втором этапе испытуемому было предложено прослушать запись «белого» шума с одновременной регистрацией параметров НМС. На третьем этапе к прослушиванию предлагалась ритмичная музыка, на четвертом – классическая музыка, на пятом – агрессивная музыка Hard Rock.
Объектом наблюдения стали 15 студентов старших курсов и аспирантов (девушек и юношей) в возрасте 21-24 лет, обучающихся в Сургутском государственном университете (СурГУ). Обследование студентов производилось неинвазивными методами и соответствовало этическим нормам Хельсинской декларации (2000 г). Критерии включения: возраст студентов 20-25 лет, отсутствие жалоб на состояние здоровья в период проведения обследований, наличие информированного согласия на участие в исследовании. Критерии исключения: болезнь студента в период обследования.
Обследования производились повторно и одновременно для правой и левой рук испытуемых. Между каждым этапом испытуемым предоставлялось время T на восстановление, T≥15 мин. Также необходимо отметить, что акустическое воздействие осуществлялось на среднем уровне громкости, при котором испытуемые не испытывали дискомфорта, связанного с высокой интенсивностью звукового потока.
Использовались датчики токовихревого типа в биофизическом измерительном комплексе (БИК), разработанном в лаборатории биокибернетики и биофизики сложных систем (ЛББСС) при СурГУ. Они обеспечивали высокую точность измерений (погрешность по вертикальной координате х1 менее 0,01 мм) и широкий линейный диапазон усиления для частот регистрируемого тремора (практически от нуля герц до 1000), а также обработку полученной информации. Принцип работы БИК заключается в использовании сигналов от двух токовихревых датчиков, между которыми помещается исследуемый объект для измерения его микроперемещений (Буров, 2010; Еськов, 2014а, 2014б Филатов, 2010,2012).
Статистическая обработка данных осуществлялась при помощи следующих программных пакетов: «Excel MS Office-2003» и «Statistica 6.1». Исследования зависимостей производились методами непараметрической статистики. Выявление различий между конкретными группами (парное сравнение групп) выполнялись при помощи непараметрического критерия Вилкоксона с поправкой Бонферрони (для оценки справедливости нулевой гипотезы). Двумерные квазиаттракторы рассчитывались по площади S=Δx1×Δx2, где Δx1 и Δx2 – вариационные размахи этих двух координат тремора (здесь x1 – вертикальная координата пальца в пространстве, х2=dx1/dt) (Адайкин, 2008; Ануфриев, 2008; Аушева, 2008; Бернштейн, 2004; Брагинский, 2006, 2010).
Результаты хаотического и энтропийного подхода в оценке параметров треморограмм
Отметим, что при квантовании треморограмм мы получали некоторые выборки x1=x1(t), которые представляли положение пальца в пространстве по отношению к датчику регистрации координаты xi (положение пальца в пространстве) в виде выборок треморограмм xi (2-6, 9-13). Далее x1(t) дифференцировался, т.е. находилась производная x2(t)=dx1/dt и получался вектор x(t)=(x1, x2)T. Вся установка включала в себя токовихревой датчик, усилители сигнала, аналого-цифровой преобразователь – АЦП и электронно-вычислительную машину – ЭВМ, которая кодировала и сохраняла информацию в виде файла, а полученные вариационные размахи по координатам x1 и х2 в виде Δx1 и Δx2 фиксировались с ее помощью по каждой выборке (в каждой серии по N=15 выборок измерений треморограмм (ТМГ).
Таблица расчета квазиаттракторов (КА) для левой и правой руки без звукового воздействия (БВ), с агрессивной музыкой (АМ), белым шумом (БШ), классической музыкой (КМ) и ритмической музыкой (РМ) представлена в табл. 1. Здесь показаны значения площади S для КА всех 15-ти испытуемых (левая и правая рука, треморограммы). Очевидны различия КА как для левой и правой руки, так и для каждого испытуемого при различных видах звуковых воздействий. Таблица 1 демонстрирует возможности применения метода расчёта КА в психофизиологических исследованиях на фоне отсутствия эффектов в рамках статистических подходов (в статистике две соседние выборки ТМГ у одного испытуемого различаются).
| Значения площадей КА - Z *10-6 (у.е.) | |||||||||
Левая рука - S (у.е.) | Правая рука - S (у.е.) | |||||||||
БВ | АМ | БШ | КМ | РМ | БВ | АМ | БШ | КМ | РМ | |
1 | 4,08 | 0,42 | 1,40 | 1,10 | 1,52 | 0,06 | 0,13 | 0,26 | 0,06 | 0,16 |
2 | 2,18 | 0,73 | 0,77 | 0,46 | 3,84 | 0,34 | 0,61 | 0,21 | 0,09 | 1,38 |
3 | 0,92 | 1,03 | 0,55 | 2,01 | 4,66 | 0,38 | 0,31 | 1,63 | 0,67 | 0,22 |
4 | 0,56 | 0,39 | 1,15 | 1,19 | 1,62 | 0,25 | 0,69 | 1,50 | 0,15 | 0,26 |
5 | 5,28 | 1,18 | 0,99 | 0,96 | 3,98 | 0,43 | 1,71 | 0,96 | 3,21 | 1,88 |
6 | 14,07 | 1,42 | 1,14 | 1,61 | 2,22 | 1,18 | 4,04 | 2,15 | 1,55 | 3,67 |
7 | 13,07 | 6,60 | 5,99 | 1,09 | 1,24 | 0,26 | 1,80 | 0,49 | 0,49 | 0,39 |
8 | 1,72 | 4,14 | 0,44 | 1,86 | 1,77 | 0,71 | 0,88 | 0,30 | 2,16 | 1,56 |
9 | 7,47 | 15,37 | 2,83 | 18,13 | 2,97 | 1,31 | 0,72 | 4,52 | 0,63 | 0,83 |
10 | 7,78 | 10,17 | 8,48 | 4,11 | 11,84 | 1,95 | 2,77 | 4,85 | 1,11 | 2,03 |
11 | 12,00 | 3,22 | 5,89 | 1,37 | 2,59 | 1,20 | 0,97 | 3,58 | 1,52 | 2,39 |
12 | 2,04 | 0,24 | 0,15 | 0,12 | 0,14 | 0,19 | 0,03 | 0,24 | 0,05 | 0,20 |
13 | 3,86 | 4,68 | 2,52 | 37,02 | 0,67 | 4,59 | 1,50 | 1,81 | 5,97 | 1,94 |
14 | 18,07 | 21,51 | 10,55 | 18,43 | 5,24 | 0,97 | 5,18 | 0,81 | 3,44 | 3,80 |
15 | 6,53 | 1,73 | 0,92 | 0,57 | 0,86 | 0,51 | 0,42 | 0,10 | 0,25 | 0,09 |
Среднее значение | 6,64 | 4,86 | 2,92 | 6,00 | 3,01 | 0,95 | 1,45 | 1,56 | 1,42 | 1,39 |
Примечание: БВ - без воздействия, АМ - агрессивная музыка, БШ - белый шум, КМ - классическая музыка, РМ - ритмичная музыка, как внешние возмущения для ВНД испытуемых. | ||||||||||
Таблица 1. Значения площадей S квазиаттракторов (КА) треморограмм левой и правой руки 15-ти испытуемых без воздействия и при различных видах звукового воздействия
Для иллюстрации последнего утверждения в табл. 2 показана матрица парного сравнения треморограмм только для одного испытуемого. Число совпадений пар выборок ТМГ из разных 105 результатов всего k=3, как для 1-го испытуемого, так и для 15-ти других разных людей (табл. 2 ипытуемый Горбунов Д.В. – ГДВ). Это означает, что все статистические функции f(x) непрерывно изменяются и статистика не дает эффекта при сравнении (хаос ТМГ). Это иллюстрирует и эффект Бернштейна «повторение без повторений» (Бернштейн, 2004) количественно. Когда мы говорим об отсутствии повторений (хаос ПФДС), это означает отсутствие произвольного повторения подряд двух или трех выборок. Последнее полностью отвергает любые статистические методы при изучении биомеханических эффектов. Это означает, фактически, что любые биомеханические измерения имеют исторический характер (артефакты). Следующая выборка дает другие f(x), СПС, автокорреляции A(t) и т.д. Сейчас необходимо пересматривать всю концепцию измерений ПФДС в психофизиологии (Еськов, 2014а, 2014б Филатов, 2010,2012; Буров, 2010; Еськов, 2014б, 2015; Козлова, 2010; Филатов, 2010,2012, 2014), если переходить к количественной характеристики в психофизиологии в рамках концепции эффекта Еськова-Зинченко.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
1 | 0.00 | 0.00 | 0.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.96 | 0.00 | 0.00 | |
2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
4 | 0.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
5 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
6 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
7 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.15 | 0.00 | |
8 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.42 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.42 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
13 | 0.96 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Таблица 2. Матрица парного сравнения выборок треморограмм испытуемого ГДВ (число повторов N=15), использовался критерий Вилкоксона (уровень значимости p<0.05, число совпадений k=3)
Одновременно в исследовании нами использовался один из методов стохастики в виде расчета значения энтропии Шеннона. Энтропия Шеннона – мера неопределенности, которая связана со случайной величиной и позволяет получить оценку уровня детерминированности/неопределенности в сигнале. Энтропия Шеннона связана с распределением вероятностей амплитуд колебаний движения. Фактически, это мера упорядоченности выборок xi – компонент ВСС x(t) в фазовом пространстве состояний (ФПС). Такая трактовка энтропии в психофизиологии сейчас может быть пересмотрена из-за вновь открывшихся закономерностей, которые мы представляем ниже.
Формальное определение энтропии для независимых случайных событий x с n возможными состояниями (от 1 до n, p – функция вероятности) рассчитывалась по формуле:
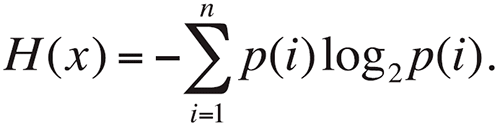
Эта процедура нами сейчас выполнялась только для одной координаты х1(t), а вторая координата (скорость) х2=dx1/dt входила в вектор х=(х1,х2)Т. Этот вектор состояния системы (ВСС) x(t) совершал непрерывные хаотические движения в таком двумерном фазовом пространстве состояний (ФПС). Само это движение у нас оценивалось в рамках расчета энтропией E (для трех групп) и параметров квазиаттракторов (КА). Причем для E мы имеем нормальное распределение (см. табл. 3), при обычном непараметрическом распределении для тремора (табл. 1 и 2) (Аушева, 2008; Бернштейн, 2004; Брагинский, 2006, 2010; Буров, 2010; Ведясова, 2012; Вохмина, 2104; Гавриленко, 2013; Добрынина, 2015; Еськов, 2009).
| Левая рука | Правая рука | ||||||||
БВ | БШ | РМ | КМ | АМ | БВ | БШ | РМ | КМ | АМ | |
1 | 3,70 | 3,78 | 3,86 | 3,73 | 3,84 | 3,81 | 3,89 | 3,67 | 3,59 | 4,13 |
2 | 3,64 | 3,94 | 3,91 | 3,62 | 3,78 | 3,86 | 3,48 | 3,65 | 3,81 | 3,54 |
3 | 3,70 | 3,70 | 3,62 | 3,75 | 3,34 | 3,73 | 3,59 | 3,75 | 3,59 | 3,97 |
4 | 3,57 | 3,83 | 4,02 | 3,64 | 3,46 | 3,62 | 3,73 | 3,51 | 3,75 | 3,46 |
5 | 3,83 | 4,02 | 3,62 | 3,51 | 3,67 | 3,57 | 3,73 | 3,75 | 3,70 | 3,57 |
6 | 3,89 | 4,13 | 3,59 | 3,89 | 4,02 | 3,70 | 3,67 | 3,73 | 3,97 | 3,78 |
7 | 3,70 | 3,56 | 3,78 | 3,54 | 3,70 | 3,38 | 3,73 | 4,02 | 3,70 | 3,32 |
8 | 3,65 | 3,56 | 3,78 | 3,78 | 3,97 | 3,81 | 3,51 | 3,53 | 3,57 | 3,75 |
9 | 3,29 | 3,59 | 3,84 | 3,73 | 3,67 | 3,13 | 3,89 | 3,70 | 3,67 | 3,61 |
10 | 3,64 | 3,86 | 3,83 | 3,62 | 3,70 | 3,51 | 3,54 | 3,38 | 3,49 | 3,94 |
11 | 3,75 | 3,89 | 3,70 | 3,67 | 3,91 | 3,97 | 3,81 | 3,83 | 3,62 | 3,70 |
12 | 3,75 | 3,54 | 3,46 | 3,97 | 3,92 | 3,62 | 3,70 | 3,78 | 3,73 | 4,10 |
13 | 3,72 | 3,72 | 3,68 | 3,75 | 3,59 | 3,76 | 3,67 | 3,49 | 3,75 | 3,91 |
14 | 3,99 | 3,78 | 3,70 | 3,89 | 3,89 | 3,86 | 3,78 | 4,05 | 3,83 | 3,67 |
15 | 3,81 | 3,51 | 3,73 | 3,59 | 3,94 | 3,89 | 3,94 | 3,89 | 3,23 | 3,73 |
Ср. знач. | 3,71 | 3,76 | 3,74 | 3,71 | 3,76 | 3,68 | 3,71 | 3,72 | 3,67 | 3,75 |
Примечание: БВ - без воздействия, БШ - белый шум, РМ - ритмичная музыка, КМ - классическая музыка, АМ - агрессивная музыка | ||||||||||
Таблица 3. Значения энтропии Шеннона E выборок треморограмм левой и правой руки без воздействия и при различных видах звукового воздействия (возмущениях)
Для выявления различий между показателями энтропии Шеннона треморограмм левой и правой рук (парное сравнение групп) использовался непараметрический критерий Вилкоксона с поправкой Бонферрони (для оценки справедливости нулевой гипотезы). Были изучены возможности статистически значимых различий при сравнении энтропии Шеннона треморограмм левой и правой руки в условиях различных акустических воздействий, которые соответствует таблице 3. Как мы установили, критерий Вилкоксона не показал различий между группами выборок энтропии Шеннона (при критическом уровне значимости р<0,05), как для левой, так и для правой рук при различных акустических воздействиях.
Таким образом, установлено, что различные акустические воздействия вызывают статистически незначимые изменения в параметрах энтропии Шеннона, хотя отмечается отдельное ее увеличение или уменьшение при этих условиях. Динамика средних значений энтропии Шеннона параметров нервно-мышечной системы (треморограмм) без акустического воздействия и с различными видами акустических воздействий для левой и правой рук испытуемых в статистическом плане слабо различается (как и для всех систем третьего типа) (Еськов, 2014а, 2014б, 2015; Козлова, 2010; Филатов, 2010,2012, 2014). Отсюда следует, что при применении статистики в изучении ПФДС мы будем иметь низкую эффективность, психофизиология требует новых подходов и методов. Мы предлагаем рассчитывать параметры квазиаттракторов при оценке особенностей высшей нервной деятельности человека. Именно параметры квазиаттракторов не дают существенных изменений при условии сохранения гомеостаза психического состояния испытуемого.
Из таблицы 1 и 3 можно видеть результаты моторной асимметрии по значениям квазиаттракторов (КА) и очень малозначимые изменения энтропии Шеннона. Для левой руки при различных видах звукового воздействия происходит увеличение энтропии Шеннона (Ебез возд =3,71; Еагр =3,76; Ебел шум=3,76; Еритм=3,74). И только при прослушивании классической музыки энтропия Шенона не изменилась (Еклас=3,71). Однако реакция правой руки на акустические воздействия несколько иная. Для правой руки происходит некоторое увеличении энтропии Шенона (Ебез возд =3,68; Еагр =3,75; Ебел шум=3,71; Еритм=3,72), а при прислушивания классической музыки произошло небольшое уменьшение энтропии (Еклас=3,67), которое статистически незначимо различается при сравнении с другими состояниями испытуемых (Буров, 2010; Ведясова, 2012; Вохмина, 2104; Гавриленко, 2013; Добрынина, 2015; Еськов, 2009, 2010; 2014а).
В целом, статистика всегда в биомеханике демонстрирует хаотический калейдоскоп статистических характеристик (f(x), СПС, A(t) и т.д.), а параметры квазиаттракторов и матрицы парных сравнений выборок дают устойчивые различия как по моторной асимметрии (левая и правая рука у нас), так и при индивидуальной характеристики испытуемых (квазиаттракторы у каждого человека специфичны), что представлены в табл. 1 (Вохмина, 2014; Гавриленко, 2013; Добрынина, 2015; Еськов, 2009, 2010; 2014а, 2014б, 2015).
Выводы:
- Любое направленное акустическое воздействие вызывает изменение в состоянии параметров НМС, об этом свидетельствуют изменения параметров квазиаттракторов, но энтропии Шеннона при этом изменяются весьма незначительно (нет статистических различий).
- При воздействии «белого» шума или агрессивной музыки реакция НМС у части испытуемых напоминает реакцию на физические нагрузки. Это говорит об определенных изменениях в спектральных реакциях треморограмм испытуемых.
- Реакции левой руки испытуемых на звуковое воздействие несколько отличается по энтропии от реакции их правой руки. Однако параметры квазиаттракторов, как реакции на звук (со стороны ВНД), различаются существенно, что отражается в параметрах моторной асимметрии. Это имеет диагностическую ценность для психофизиологии и может использоваться на практике для выявления индивидуальных особенностей такой моторной асимметрии.
Литература:
- Адайкин В.И. Стохастические и хаотические подходы в оценке влияния метеофакторов на заболеваемость населения на примере ХМАО- Югры / В.И. Адайкин, К.Н. Берестин, А.А. Глущук и др. // Вестник новых медицинских технологий. – 2008. – Т. 15. – № 2. – С. 7-9.
- Ануфриев А.С. Медико-биологическая трактовка понятия стационарнных режимов биологических динамических систем / А.С. Ануфриев, В.М. Еськов, А.Г. Назин и др. // Вестник новых медицинских технологий. – 2008. – Т. 15. – № 1. – С. 29-32.
- Аушева Ф.И. Системный анализ суточной динамики показателей сердечно-сосудистой системы у больных при артериальной гипертензии / Ф.И. Аушева, И.Ю. Добрынина, Е.А. Мишина и др. // Вестник новых медицинских технологий. – 2008. – Т. 15. – № 4. – С. 208-210.
- Бернштейн Н.А. Биомеханика и физиология движений : избр. психол. труды / Н.А. Бернштейн ; под ред. В.П. Зинченко. – Москва :Изд-во Моск. психол.-соц. ин-та ; Воронеж : МОДЭК, 2004. – 687 с. : ил., табл.
- Брагинский М.Я. Влияние хаотической динамики метеофакторов на показатели кардио-респираторной системы человека в условиях Севера / М.Я Брагинский, В.М. Еськов, С.Н. Русак и др. // Вестник новых медицинских технологий. – 2006. – Т. 13. – № 1. – С. 168-170.
- Брагинский М.Я. Исследование функциональных систем организма студентов Югры в условиях мышечной нагрузки методом фазового пространства / М.Я. Брагинский, А.А. Балтикова, В.В. Козлова и др. // Современные наукоемкие технологии. – 2010. – № 12. – С. 23-24.
- Буров И.В. Анализ параметров психофизиологических функций учащихся Югры с помощью методов многомерных фазовых пространств / И.В. Буров, М.А. Филатов, Д.Ю. Филатова и др. // Современные наукоемкие технологии. – 2010. – № 12. – С. 12-13.
- Ведясова О.А. Биоинформационный анализ макро-хаоса и микродинамического хаоса в биологических системах / О.А. Ведясова, С.С. Беднаржевский, Д.В. Синенко и др. // Вестник новых медицинских технологий. – 2012. – Т. 19. – № 2. – С. 410-411.
- Вохмина Ю.В. Стационарные режимы поведения сложных биосистем в рамках теории хаоса-самоорганизации / Ю.В. Вохмина, Л.М. Полухин, Л.М. Бикмухаметова и др. // Вестник новых медицинских технологий. – 2014. – Т. 21. – № 1. – С. 141-144.
- Гавриленко Т.В. Метод многомерных фазовых пространств в оценке хаотической динамики тремора / Т.В. Гавриленко, А.Е. Баженова, А.А. Балтикова и др. // Вестник новых медицинских технологий. – 2013. – № 1. – С. 5.
- Добрынина И.Ю. Особенности кардиоинтервалов: хаос и стохастика в описании сложных биосистем / И.Ю. Добрынина, Д.В. Горбунов, В.В. Козлова и др. // Вестник новых медицинских технологий. – 2015. – Т. 22. – № 2. – С. 19-26.
- Еськов В.М. Математическое моделирование непроизвольных движений в норме и при патологии / В.М. Еськов, В.В. Полухин, В.Ю. Дерпак и др. // Сложность. Разум. Постнеклассика. – 2015. – № 2. – С. 75-86.
- Еськов В.М. Метод системного синтеза на основе расчета межаттракторных расстояний в гипотезе равномерного и неравномерного распределения при изучении эффективности кинезитерапии / В.М. Еськов, В.В. Еськов, А.А. Хадарцев и др. // Вестник новых медицинских технологий. – 2010. – Т. 17. – № 3. – С. 106-110.
- Еськов В.М. Насколько экономически эффективно внедрение методов теории хаоса и синергетики в здравоохранение / В.М. Еськов, В.И. Адайкин, Ю.В. Добрынин и др. // Вестник новых медицинских технологий. – 2009. – Т. 16. – № 1. – С. 25-28.
- Еськов В.М. Новый метод использования нейроэмуляторов в психофизиологии / В.М. Еськов, В.В. Еськов, Д.Ю. Филатова и др. // Вестник новых медицинских технологий. – 2014а. – Т. 21. – № 3. – С. 7-12.
- Еськов В.М. Системный анализ, управление и обработка информации в биологии и медицине / В.М. Еськов, А.А. Хадарцев, В.В. Козлова и др. // Системный синтез параметров функций организма жителей Югры на базе нейрокомпьютинга и теории хаоса-самоорганизации в биофизике сложных систем . Том XI. –Самара : Офорт, 2014б. – 192 с.
- Козлова В.В. Измерение Расстояний между центрами квазиаттракторов вектора состояния организматренированных и нетренированных г.Самары и г.Сургута / В.В. Козлова, В.Н. Голушков, О.А. Ведясова и др. // Ученые заметки ТОГУ. – 2010. – Т. 1. – № 1. – С. 27-30.
- Филатов М.А. Идентификация параметров порядка в психофизиологии / М.А. Филатов, Д.Ю. Филатова, Д.А. Сидоркина и др. // Сложность. Разум. Постнеклассика. – 2014. – № 2. – С. 4-13.
- Филатов М.А. Метод матриц межаттракторных расстояний в идентификации психофизиологических функций человека / М.А. Филатов, Д.Ю. Филатова, О.А. Химикова и др. // Сложность. Разум. Постнеклассика. – 2012. – № 1. – С. 20-24.
- Филатов М.А. Метод фазовых пространств в моделировании психофизиологических функций учащихся Югры : монография. – Самара, 2010.





