Линейные модели со смешанными эффектами в когнитивных исследованиях


Published: March 21, 2015
Latest article update: Sept. 15, 2022
Abstract
Анализ данных в когнитивных исследованиях всегда сопряжен с определенными трудностями: отсутствие полностью сбалансированного дизайна, невозможность подобрать полностью эквивалентные стимулы, пропущенные значения в ответах и т. д. Для контроля случайной ошибки чаще всего применяется усреднение данных по испытуемым либо стимулам, а после этого усредненные данные анализируются с помощью традиционных методов, таких как дисперсионный анализ. В статье рассматривается альтернативный подход, основанный на применении регрессионных моделей со смешанными эффектами. Этот вид моделей позволяет анализировать данные без усреднения, включая в модель в явном виде допущения о существующих между отдельными наблюдениями взаимосвязях. В качестве примера анализа используются результаты квазиэксперимента, в котором оценивается связь времени ответа в задаче узнавания с правильностью ответа, полом испытуемого и полом человека на предъявленной фотографии. Сравнение результатов анализа с помощью смешанных моделей и различных вариантов дисперсионного анализа (с усреднением по стимулам, по испытуемым и без усреднения) показывает схожесть результатов смешанных моделей с результатами дисперсионного анализа по испытуемым и результатами дисперсионного анализа по наблюдениям. Однако в случае смешанных моделей интерпретация результатов становится более обоснованной, так как и различия между стимулами, и различия между испытуемыми включены в модель. В заключении рассматриваются преимущества смешанных моделей и даются рекомендации по выбору случайных эффектов для включения в модель.
Keywords
Регрессионный анализ, квазиэксперимент, смешанные модели, время реакции, ошибки, дисперсионный анализ
Введение
В психологическом эксперименте основным объектом интереса являются различия в значении зависимой переменной между уровнями одной или нескольких независимых переменных. Все остальное — температура в помещении, время суток, индивидуальные различия испытуемых, свойства стимулов и множество других факторов — считаются «шумом» или случайной ошибкой, влияния которой экспериментатор старается избежать всеми доступными способами. Для этого испытуемые случайным образом распределяются между группами, стимулы — между условиями, испытуемые изолируются от внешних факторов в лаборатории, применяется специальное оборудование, увеличивается количество наблюдений или опытов, а также используются другие методические приемы, хорошо известные любому исследователю. После сбора данных наступает пора их анализа. В идеальной ситуации перед исследователем предстает прекрасная картина сбалансированного дизайна, в котором отсутствуют пропущенные значения, количество измерений для каждой комбинации испытуемого и независимых переменных достаточно велико и все измерения проводились в одних и тех же условиях.
В реальности, разумеется, ситуация отличается. Появляются пропущенные значения, например, часто из анализа исключаются ошибочные ответы испытуемого, выясняется, что из-за усталости и научения испытуемого количество наблюдений достаточно ограничено, на предполагавшиеся одинаковыми стимулы испытуемые дают разные реакции и т. д. Хуже всего дело обстоит в тех случаях, когда какие-либо переменные оказываются неподконтрольными экспериментатору. Например, пытаясь изучить связь между частотой употребления слова и вероятностью его опознания при краткосрочном предъявлении, исследователь может сколь угодно долго выравнивать группы часто- и редкоупотребляемых слов по всем характеристикам, однако в результате перед ним все равно окажутся разные группы слов. Профессиональная область интересов автора связана с изучением ошибок и эмоциональных реакций, и, как можно предположить, и то, и другое в достаточно слабой степени может контролироваться экспериментатором.
Подобные ситуации возникают наиболее часто в квазиэкспериментальных исследованиях, однако и в других видах исследований может быть полезно учесть влияние переменных, которые невозможно контролировать. Например, данные в сбалансированном психофизическом эксперименте будут тем не менее подвержены влиянию научения и усталости, то есть будет влиять порядковый номер пробы. Психологи, проводящие исследования в школах, могут захотеть учесть различия между испытуемыми, набранными в разных классах или разных школах. Физиологические данные, собираемые в лонгитюдных исследованиях, могут различаться в зависимости от времени суток и т. д.
Классическим методом для контроля ошибки в ситуациях, когда невозможно отделить независимую переменную от испытуемого (иногда подобные переменные также называют субъектными) или стимула, являются тесты для двух связанных выборок и дисперсионный анализ (ANOVA) с повторными измерениями. Однако у анализа с повторными измерениями есть некоторые недостатки. Во-первых, часто оказывается неочевидным, что нужно выбрать в качестве единицы анализа. Например, при анализе реакций испытуемого на разные стимулы в зависимости от экспериментальных условий можно использовать в качестве единицы анализа как стимул, так и испытуемого. Чаще всего в таких ситуациях предлагается проводить анализ после усреднения реакций «по стимулам» или «по испытуемым». Однако при усреднении будет потеряна часть данных. Более того, у нас нет никаких оснований для того, чтобы выбрать из этих двух вариантов более оптимальный. По этой причине в психолингвистических исследованиях рекомендуется приводить результаты обоих вариантов анализа и рассчитывать на их основе критерий minF": minF’ = (F1+F2)/F1*F2, где Fl и F2 относятся к результатам анализа по испытуемым и по стимулам соответственно (Clark, 1973; Raaijmakers et al., 1999; Raaijmakers, 2003).
Смешанные линейные модели
Возможной альтернативой дисперсионному анализу с повторными измерениями является регрессионный анализ с использованием смешанных линейных моделей. Сущность данного метода заключается в следующем. Предполагается, что эффекты (факторы), оказывающие влияние на зависимую переменную, можно условно разделить на два типа: фиксированные и случайные. Хотя по поводу философских и методологических аспектов разделения эффектов на фиксированные и случайные идут споры (Gelman, 2005; r-sig-mixed- models FAQ-GLMM, 2015), в данной работе я буду рассматривать как случайные те эффекты, которые случайным образом варьируются в исследовании и не отражают все возможные значения фактора в генеральной совокупности. Фиксированные эффекты, с другой стороны, — это то, что обычно является предметом интереса исследователя, то есть те независимые переменные, уровни которых он устанавливает или контролирует. С практической точки зрения необходимо также учитывать, что для оценки случайных эффектов необходимо, чтобы количество уровней соответствующего фактора было относительно велико — 5-6 уровней минимум (r-sig-mixed-models FAQ-GLMM, 2015).
По сути смешанные модели — это расширение регрессионных моделей. Обычная линейная регрессионная модель выглядит следующим образом:
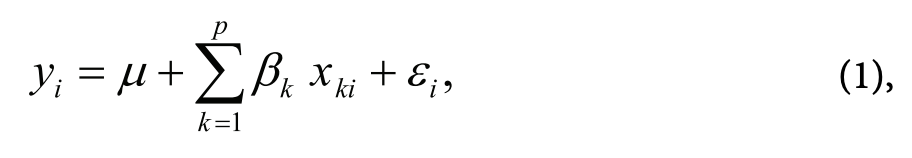
где yj — значение зависимой переменной для r'-ro наблюдения, р — константа, ßk — значение коэффициента для к-го фактора, хкі — значение к-го фактора для r'-ro наблюдения, е, — значение остатка для г-го наблюдения.
Возьмем для примера простой эксперимент с задачей лексического решения, где время ответа измеряется в зависимости от типа стимула (слово - не слово) и количества букв в стимуле. Тогда у, будут обозначать время ответа в каждой пробе, ß} — различие по времени ответа между словом и не словом, хц — тип стимула в данной пробе, ß2 — изменение времени ответа при увеличении длины слова на одну букву, х2і — длину слова в данной пробе, е, — отличие времени ответа, предсказанного на основе модели, от реального.
В случае смешанных моделей уравнение меняется следующим образом:
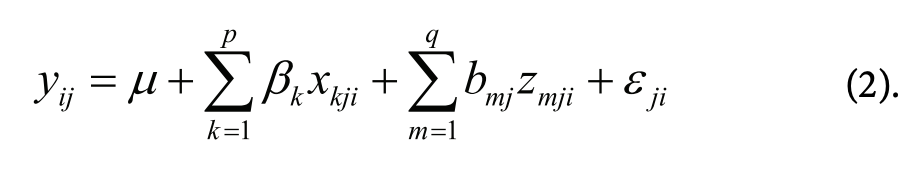
В отличие от ß, коэффициентов для фиксированных эффектов, которые одинаковы для всех наблюдений, коэффициенты для случайных эффектов, Ь, определены для j-й группы наблюдений, а zmji задает значение случайного эффекта для данной группы и данного наблюдения. Продолжая пример, допустим, каждая группа наблюдений — отдельный испытуемый и случайный эффект для каждого испытуемого только один — константа. Тогда bj — среднее1 (Корректнее было бы говорить о предсказанном среднем отклонении времени ответа испытуемого, но для краткости здесь и далее — среднее.) отклонение времени ответа для данного испытуемого от общегруппового среднего, а — идентификатор испытуемого.
Группой наблюдений может являться не только испытуемый, но и стимул, или и то, и другое. Другими словами, можно предположить, например, что каждому испытуемому или стимулу соответствует свое время ответа, то есть наличие случайного свободного члена в уравнении регрессии. Кроме того, можно также предположить, что время правильных и неправильных ответов у разных испытуемых различается или различается время ответа на мужские лица в сравнении с женскими, то есть предположить случайный эффект наклона прямой регрессии для каких-либо внутригрупповых факторов. В случае более сложных дизайнов исследования испытуемые сами могут быть объединены в какие-то большие группы, например, школы или больницы, и тогда в уравнение регрессии добавляется еще один уровень.
Основное требования к данным в случае смешанных моделей — наличие групп взаимосвязанных наблюдений. В дополнение к этому смешанные линейные модели требуют тех же допущений, что и обычные линейные модели:
- Эффекты в модели аддитивны, то есть влияние одного предиктора не зависит от уровня другого предиктора. Если это требование нарушается, необходимо преобразование переменных или включение в модель взаимодействий.
- Линейная взаимосвязь между независимыми и зависимой переменной. Случаи нелинейной связи также можно анализировать, преобразовав переменные или включив в модель полином (х+х2+х3+...).
- Ошибки (остатки) имеют равную дисперсию и распределены нормально. Это наименее важные из ограничений, практически никогда не соблюдаемые на практике, и их нарушения обычно не приводят к существенным проблемам (Gelman, Hill, 2007).
Независимость ошибок, существенная для обычных линейных моделей, в случае смешанных моделей не обязательна (Pinheiro, Bates, 2000). Более того, отдельные статистические пакеты, например, nlme (Sarkar et al., 2008), позволяют легко задавать структуру взаимосвязей ошибок в явном виде, хотя эта тема выходит за пределы данной статьи.
Кроме того, число наблюдений должно быть не меньше числа уровней случайных эффектов в модели для того, чтобы анализ с помощью смешанных моделей стал возможен хотя бы теоретически. Например, если речь идет об испытуемых как случайном эффекте и в модели также присутствует случайный эффект для взаимодействия испытуемого и какого-либо еще фактора, то число наблюдений должно быть не меньше, чем число испытуемых, умноженное на число уровней фактора. Проводя аналогию с классическими тестами, провести тест Стьюдента для двух связанных выборок невозможно, если число наблюдений для каждого испытуемого меньше двух. Однако это лишь ограничение на применимость метода: осмысленность и надежность полученных результатов будет тем выше, чем больше наблюдений анализируется.
Как и для других регрессионных моделей, для смешанных моделей предикторами могут выступать как количественные (включая ранговые), так и категориальные переменные. Зависимая переменная также может измеряться в различных шкалах при условии, что для нее указано соответствующее распределение. Отдельно стоит отметить, что для биномиальных данных (в том числе точности ответов) использование смешанных биномиальных моделей приводит к более точным оценкам, чем дисперсионный анализ (Jaeger, 2008). Для ранговых переменных можно использовать порядковую регрессию со смешанными эффектами, например, с помощью пакета DPpackage (Jara et al., 2011), хотя во многих случаях вполне оправданным будет применение обычных смешанных моделей.
Благодаря подобным возможностям смешанные модели в последние годы начинают использоваться в различных областях: в психолингвистике (Mousikou et al., 2015), в исследованиях восприятия и внимания (Kristjänsson, Jöhannesson, 2014; Laubrock et al., 2008; Королькова, 2014), в работах по проблеме сознания (Sandberg et al., 2010), в социальной психологии (Biesanz, Human, 2010; Wright et al., 2010), в мета-ана- лизе (Bakker, Wicherts, 2011), в исследованиях памяти (Oberauer, Kliegl, 2006; Wright, London, 2009), клинической психологии (Baldwin et al., 2009), психофизиологии (Gulbinaite et al., 2014; Wu, Clark, 2014) и т.д.
Сложность применяемых моделей также разнится. Например, Сэндберг и коллеги (Sandberg et al., 2010) сравнивали различные шкалы осознанности, используя внутригрупповой дизайн и контролируя избыточную дисперсию между испытуемыми через включение в модель случайного эффекта для испытуемых. Мусику и коллеги (Mousikou et al., 2015) исследовали влияние прайминга в задаче лексического решения и включали в модель случайные эффекты для испытуемого, стимула и типа прайма с группировкой по стимулу. Четвериков (Chetverikov, 2014) использовал смешанную модель для контроля вариативности стимулов и индивидуальных различий между испытуемыми в задаче оценки привлекательности лиц. Применяются и более сложные модели. Например, в работе Болдуина и коллег (Baldwin et al., 2009) рассматривалась эффективность психотерапии с включением случайного эффекта пациента, линейного и квадратичного эффектов количества психотерапевтических сессий с группировкой по пациенту, эффекта психотерапевта и линейного эффекта количества сессий с группировкой по психотерапевту.
При этом количество статей с использованием смешанных моделей постоянно увеличивается. На момент написания этой статьи Google Scholar по запросу «“mixed effects model” psychology» выдавал 1150 результатов за 2012 год, 1440 — за 2013 год, и 1890 — за 2014. Далеко не все авторы упоминают применяемый метод именно с формулировкой “mixed effects model”, поэтому реальное число статей с использованием смешанных моделей еще выше.
В оставшейся части статьи я описываю различия в подходах и результатах обработки квазиэксперимен- тальных данных с помощью дисперсионного анализа и смешанных регрессионных моделей на примере реального исследования.
Анализ времени ответа в квазиэксперименте
Дисперсионный анализ с усреднением по испытуемым/стимулам
Рассмотрим следующий квазиэксперимент. Использовалась задача узнавания: испытуемому на краткий промежуток времени предъявляется фотография лица, затем через какое-то время эта фотография предъявляется вместе с другой, новой, и испытуемого просят выбрать фотографию, которую он уже видел ранее. Исследователя интересует, как соотносится между собой время правильных и неправильных ответов. Правильность ответа испытуемого невозможно задать экспериментально, не влияя на другие параметры задачи. Например, можно сделать так, что будут только неправильные ответы, сделав задачу практически нерешаемой, но это будет уже фактически другая задача. Поэтому в данном случае речь идет о классическом квазиэксперименте: независимая переменная «правильность ответа» не контролируется экспериментатором. Кроме того, ему необходимо учитывать фактор пола испытуемого и пола человека на фотографии (фактор, далее обозначаемый как тип стимула), так как есть предположение, что данные факторы могут помешать корректной оценке эффекта правильности ответа в генеральной совокупности.
Есть несколько возможных вариантов проведения дисперсионного анализа: анализ «по испытуемым», «по стимулам» и «по наблюдениям». В первом случае рассчитывается среднее для каждого испытуемого по каждому типу стимула, во втором случае, наоборот, рассчитывается среднее для каждого стимула по каждому типу испытуемых. Эти виды анализа особенно проблематичны в случаях, подобных рассматриваемому, поскольку распределение стимулов по правильным и неправильным ответам не является случайным, а определяется сочетанием свойств испытуемого и стимула. Наконец, в третьем случае можно отказаться от анализа с повторными изменениями в пользу обычного дисперсионного анализа в надежде, что избыточная дисперсия будет скомпенсирована увеличением количества измерений за счет отсутствия усреднения.
Для данной статьи я использовал данные эксперимента, цель которого не заключалась в анализе эффекта правильности ответов, но который тем не менее позволяет провести подобный анализ. В рамках данного эксперимента по описанной выше процедуре испытуемые (N = 60) выполняли 43 пробы каждый. Всего использовалось 86 стимулов, для каждого испытуемого 43 из них выбирались случайным образом. Таким образом, набор данных состоял из 2580 наблюдений (данные доступны для анализа в онлайн-приложении к статье).
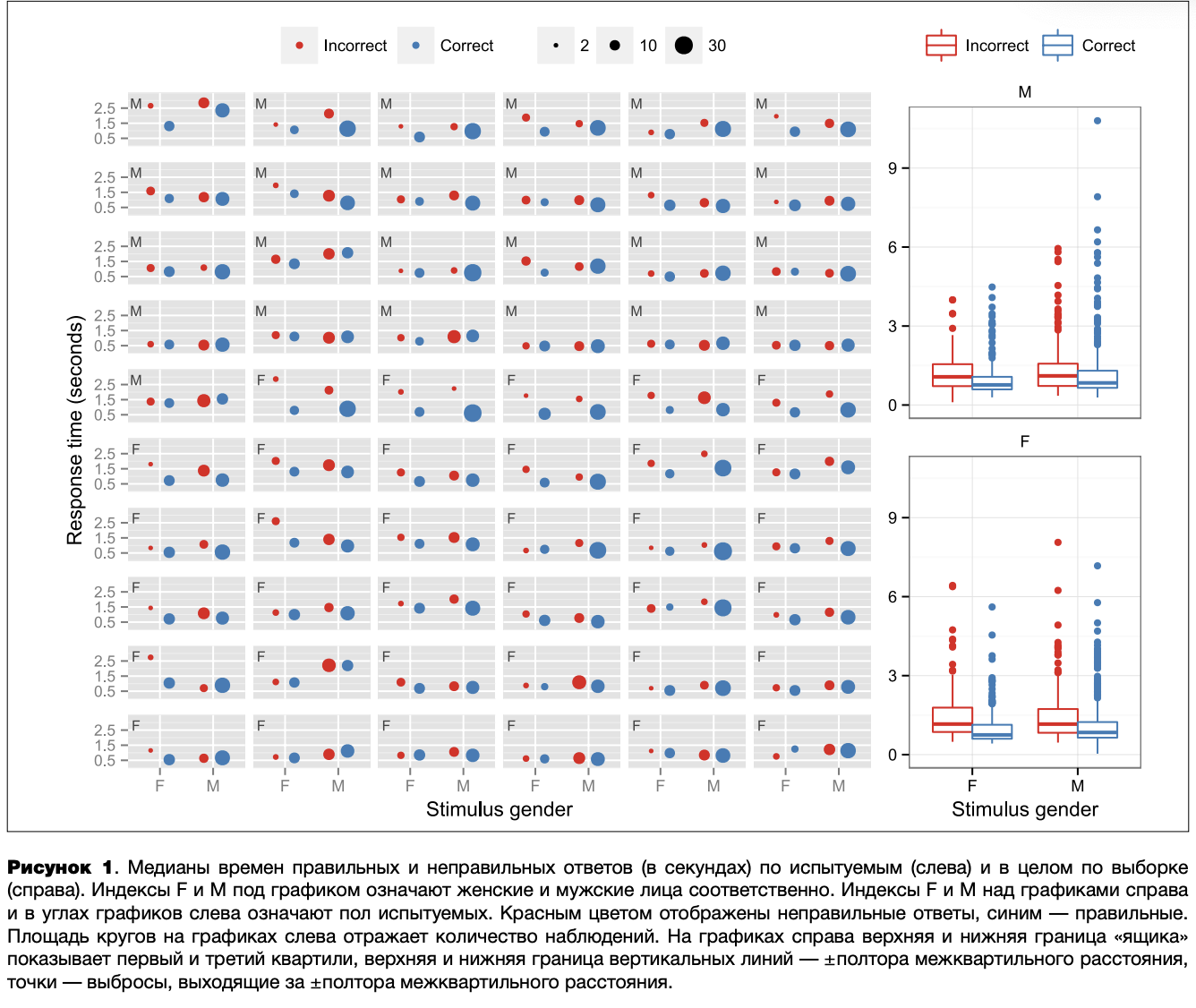
На рисунке 1 приведены медианы времен ответов в зависимости от пола испытуемого, типа стимула и правильности ответа. Как видно из данного графика, распределение ответов достаточно сильно отличается от равномерного. Мужских фотографий предъявлялось больше, чем женских (это связано с соотношением числа мужских и женских фотографий в использовавшейся базе стимулов), правильных ответов заметно больше, чем неправильных. В результате у испытуемых номер 5,6,16,19,24,28 практически нет неправильных ответов при предъявлении женских фотографий. Анализ распределения времен правильных и неправильных ответов в целом по группе (правая часть графика) позволяет предположить, что будет выражен эффект правильности ответа и, возможно, типа стимула.
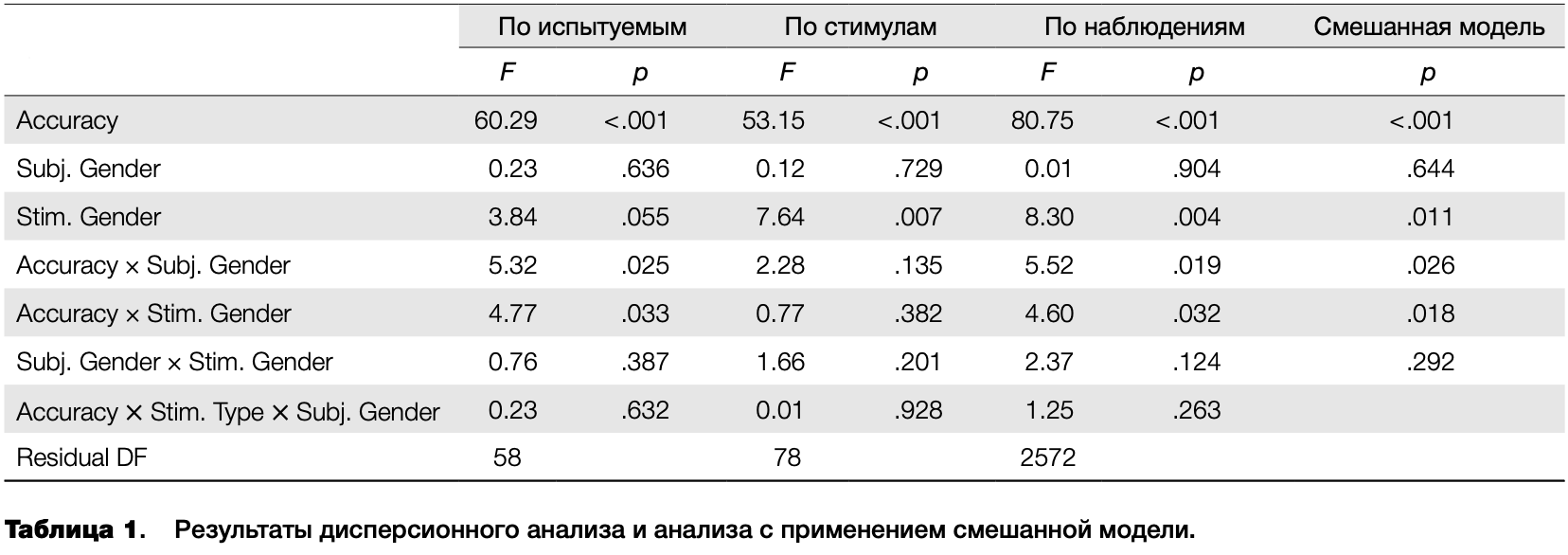
Попробуем сначала провести дисперсионный анализ с усреднением данных «по испытуемым» и «по стимулам». Анализ проводился в системе статистических вычислений R (R Core Team, 2014) с применением суммы квадратов типа II и контрастов с нулевой суммой (sum-to-zero). Результаты анализа приведены в таблице 1. Здесь и далее переменные обозначены следующим образом: пол испытуемого — Subject Gender, тип стимула — Stimulus Gender, правильность ответа — Accuracy. Взаимодействия переменных обозначены через «х». Статистически значимыми оказались эффекты правильности ответа и взаимодействия правильности ответа и типа стимула. Кроме того, на уровне тенденции проявился основной эффект типа стимула. При попытке провести анализ «по стимулам» оказалась, что для 6 из 86 стимулов не хватает данных, т.е. для них не представлены те или иные комбинации пола испытуемого и правильности ответа. Результаты анализа по оставшимся стимулам представлены в таблице 1. Как можно заметить, они сильно отличаются от анализа «по испытуемым» — значимыми остались только эффекты типа стимула и правильности ответа.
Далее я использовал третий подход — дисперсионный анализ «по наблюдениям», без усреднения. Хотя при использовании этого подхода отсутствует потеря данных вследствие усреднения, возникает опасность того, что результаты будут искажены из-за несбалансированности данных. Например, низкая средняя точность и скорость ответов нескольких отдельно взятых испытуемых может привести к тому, что будет проявляться снижение скорости неправильных ответов по всей выборке. Кроме того, не учитывается взаимосвязь результатов каждого испытуемого, то есть нарушается допущение дисперсионного анализа о независимости измерений. Как видно из таблицы 1, результаты дисперсионного анализа сырых данных согласуются с результатами анализа «по испытуемым», но не согласуются с результатами анализа «по стимулам».
Смешанные линейные модели
В смешанную регрессионную модель были включены шесть фиксированных эффектов: пол испытуемого, тип стимула, правильности ответа и их взаимодействия второго уровня. Кроме того, в модель были включены четыре случайных эффекта: (1) испытуемого; (2) случайного угла наклона для правильности ответа по испытуемым; (3) стимула; (4) случайного угла наклона для пола испытуемого по стимулам.
Данная модель предполагает, что испытуемые отличаются по среднему времени ответа и могут по- разному реагировать на стимулы разного пола и что время ответа на конкретные стимулы также отличается и может быть различным в зависимости от пола испытуемого. Я не включал в модель взаимодействие третьего уровня, так как все три предшествующих анализа показали, что оно не значимо, а его исключение упрощает расчеты модели.
Для проведения анализа была использована библиотека Ime4 (Bates et al., 2014). В R существует несколько альтернативных библиотек для анализа смешанных моделей, однако наиболее легкой в использовании представляется именно эта. Современные версии других программ для статистических расчетов, таких как STATA, SAS и SPSS, также включают в себя команды для регрессионного анализа со смешанными моделями (краткое сравнение статистических пакетов для смешанных моделей можно найти здесь: GLMM package comparison, 2015; r-sig-mixed-models FAQ- GLMM, 2015).
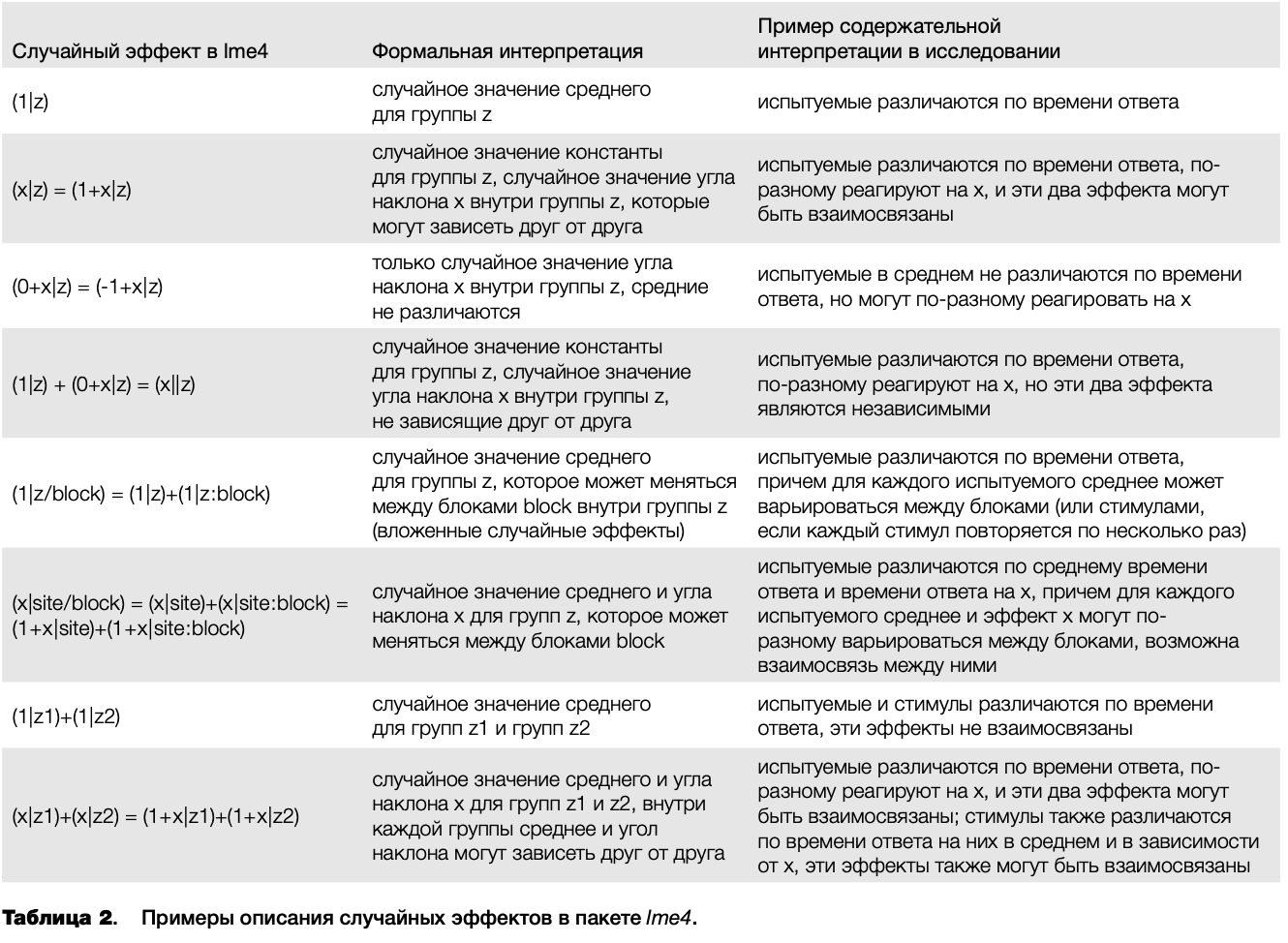
В Ime4, как и во многих других пакетах в R, для задания модели используется синтаксис в виде «формулы», схожей с регрессионным уравнением. Например, для модели, включающей фиксированный эффект для х, фиксированный эффект для z и случайный эффект для х и среднего с группировкой по испытуемым, формула будет выглядеть как y~x + z+ (x \ Subject). Здесь видно, что зависимая переменная отделяется от предикторов тильдой, предикторы разделяются знаком плюс, а группировка случайных эффектов задается в скобках с вертикальной чертой, отделяющей группирующую переменную. Случайные и фиксированные эффекты для среднего (Intercept) предполагаются по умолчанию, поэтому в явном виде их указывать необязательно. В таблице 2 представлены примеры формул для записи некоторых часто встречающихся вариантов случайных эффектов в Іте4.
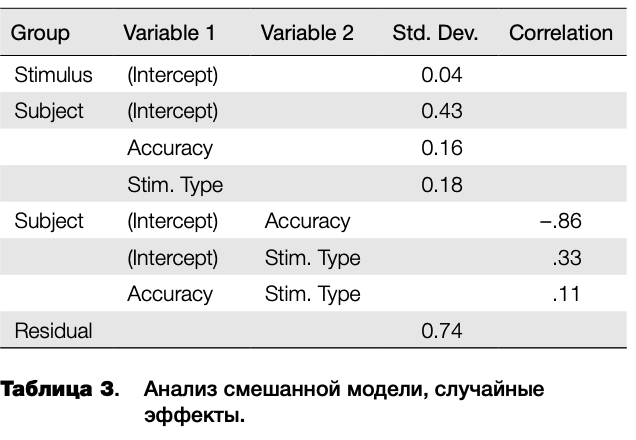
Смешанная модель (Акаіке information criterion, АІС = 5999) в целом лучше описывала данные, чем простой дисперсионный анализ без усреднения (АІС = 6500). Сначала рассмотрим данные о случайных эффектах. В таблице 3 в первом столбце представлены данные о «группах» случайных эффектов. В полученной модели случайные эффекты разбиты на две группы: к первой группе (Stimulus) относится только эффект стимула, ко второй (Subject) — эффект испытуемого и эффекты разного угла наклона прямой регрессии по испытуемым для правильных и неправильных ответов (Accuracy) и стимулов разного типа (Stimulus Туре). В данной модели были применены уровневые (treatment) контрасты. В четвертом и пятом столбцах показаны стандартные отклонения и корреляции между случайными эффектами. Доля изменчивости по испытуемым (.43) значительно выше, чем по стимулам (.04). Это означает, что время ответа в значительно большей степени варьируется между испытуемыми, нежели между стимулами.
Кроме того, существует высокая негативная корреляция (-.86) между случайным эффектом испытуемого (Intercept) и случайным эффектом для правильности ответа по испытуемым (Accuracy). В то же время взаимосвязь случайного эффекта испытуемого и случайного эффекта типа стимула по испытуемым низкая (.33). Поскольку используются уровневые контрасты, то случайный эффект Intercept в данной модели отражает сдвиг времени ответа испытуемого относительно группового среднего при условии, что ответ неправильный (Accuracy = 0) и предъявлена фотография женщины (Stimulus Туре = F). Это затрудняет непосредственный анализ обнаруженной негативной корреляции.
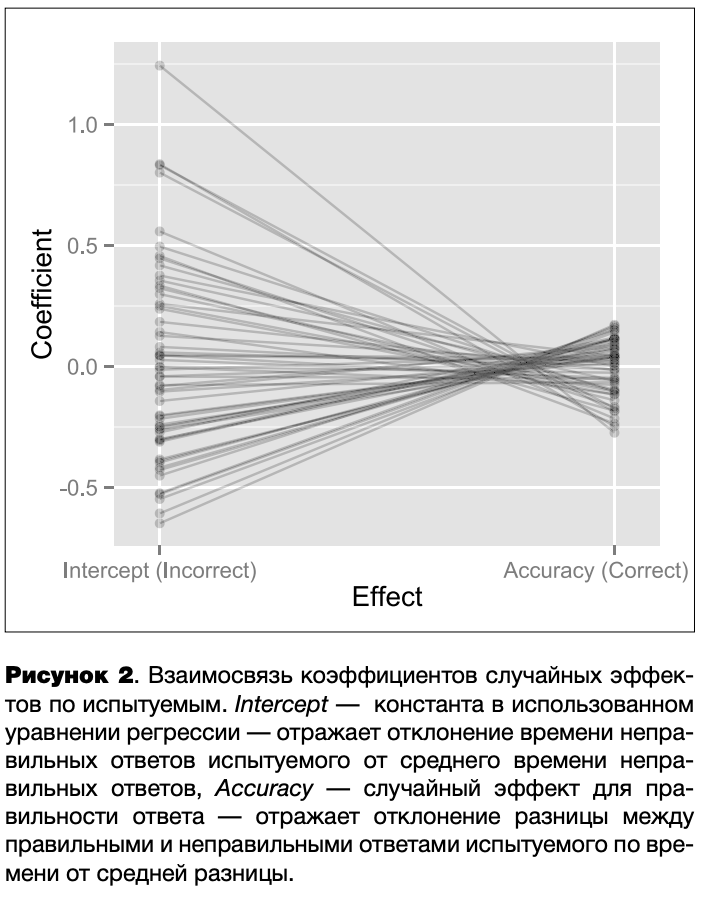
Для того чтобы прояснить ее природу, был проведен повторный анализ с исключением случайного эффекта взаимодействия испытуемого и типа стимула. Корреляция эффектов Intercept и Accuracy осталась высокой (-.76). Поскольку в модели осталось всего два случайных эффекта для испытуемого, можно говорить о том, что время неправильных ответов негативно взаимосвязано с различием времени правильных и неправильных ответов. Иначе говоря, если неправильные ответы испытуемого медленнее неправильных ответов по группе (значение Intercept будет соответственно выше), то разница по времени правильных и неправильных ответов будет меньше. Эта взаимосвязь отражена на рисунке 2.
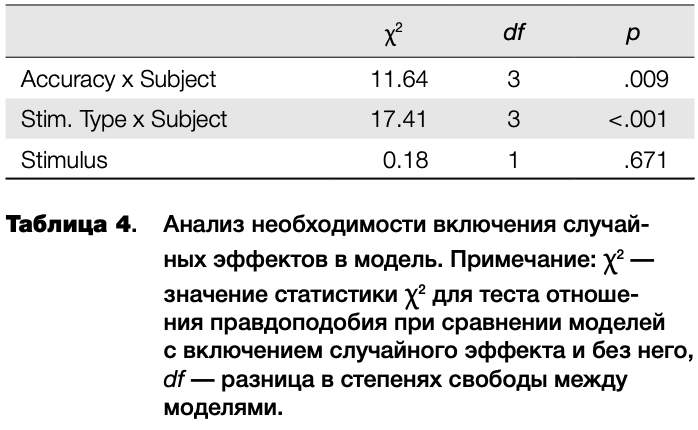
Применение смешанных моделей позволяет узнать, насколько необходимо добавление случайного эффекта, путем сравнения моделей с включенным и исключенным случайным эффектом. В таблице 4 представлены результаты такого сравнения для случайных эффектов угла наклона прямой регрессии по испытуемым и эффекта стимула. Удаление эффекта стимула не приводит к значимым различиям в объяснительной силе модели, в отличие от эффектов угла наклона. Это неудивительно, учитывая низкие значения диспер
сии эффекта стимула (таблица 3). Поэтому данный эффект можно было бы исключить из дальнейшего анализа, но поскольку эффекты для включения в модель выбирались исходя из теоретических соображений, дальнейший анализ также проводился с включением случайного эффекта стимула.
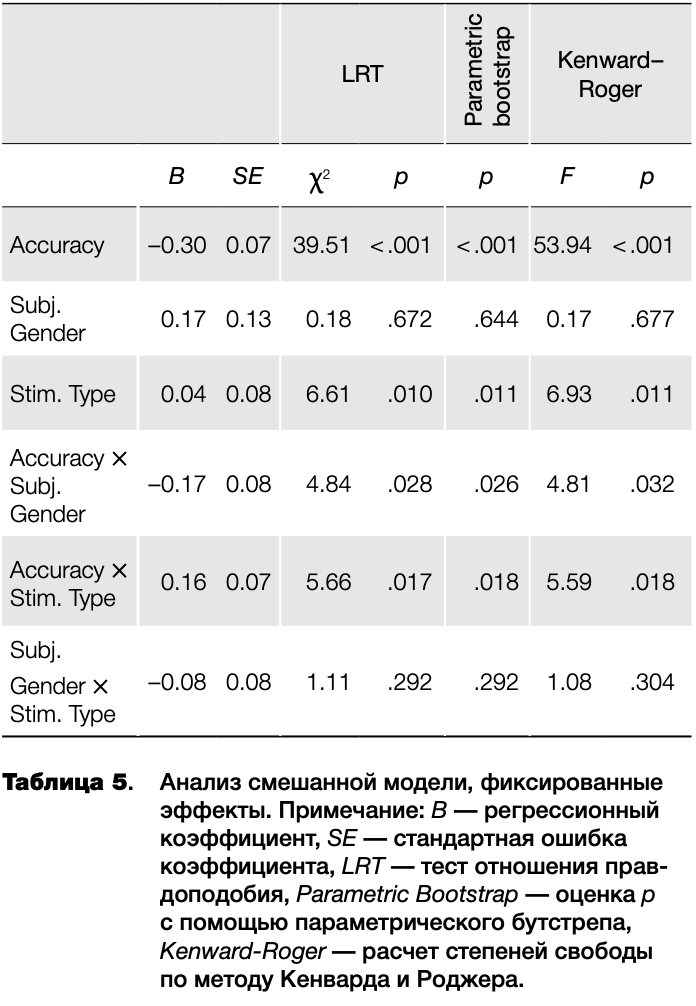
Значения фиксированных эффектов для итоговой модели представлены в таблице 5. В библиотеке Іте4 не реализован расчет р-уровней для моделей с гауссовым распределением зависимой переменной, что обусловлено теоретической неоднозначностью расчетов числа степеней свободы (Bates, 2006). Тем не менее существуют возможные пути решения данной проблемы, в частности:
- Сравнение моделей на основе отношения правдоподобия (likelihood ratio test, LRT).
- Оценка значимости с расчетом степеней свободы с использованием аппроксимации по методу Кен- варда-Роджера, реализованная в библиотеке pbkrtest (Halekoh, Hojsgaard, 2014).
- Параметрические методы бутстрепа, также реализованные в библиотеке pbkrtest.
- Оценка значимости с расчетом степеней свободы с использованием аппроксимации по методу Саттерту- эйта, реализованная в библиотеке ImerTest для проверки гипотез с использованием суммы квадратов типа III (Kuznetsova et al., 2014).
LRT обычно считается менее надежным подходом, чем аппроксимация по методу Саттертуэйта, которая в свою очередь менее надежна, чем метод Кенварда- Роджера или параметрический бутстреп (r-sig-mixed- models FAQ-GLMM, 2015).
Я использовал три первых метода. Сравнение моделей производилось по аналогии с вычислением суммы квадратов типа II в дисперсионном анализе. Все методы расчета р-уровня показали практически идентичные результаты.
Таким образом, результат применения смешанных моделей оказался близок к результатам дисперсионного анализа «по испытуемым» и результатам анализа сырых данных, что говорит о надежности данного метода.
Заключение
Когда есть вероятность влияния различий между стимулами или между испытуемыми на полученные эффекты, для анализа данных можно применить несколько подходов. Дисперсионный анализ «по стимулам» позволяет учесть различия между стимулами, однако не учитываются различия между испытуемыми. Анализ «по испытуемым» позволяет учесть различия между испытуемыми, но теряются различия между стимулами. При этом в обоих случаях используется предварительное усреднение данных, что потенциально может приводить к потерям в мощности анализа. Дисперсионный анализ сырых данных не имеет проблем с потерей мощности в результате усреднения, но и не учитывает наличия связанных групп наблюдений. Смешанные модели позволяют учесть оба типа различий. Это не сделает квазиэксперимент экспериментом, но снижает вероятность получения результатов, искаженных за счет различий между стимулами или различий между испытуемыми. Кроме того, даже в обычном эксперименте это позволит проконтролировать возможное влияние побочных переменных.
Проведенное сравнение методов на материале квазиэксперимента с измерением времени ответа показывает, что результаты анализа с помощью смешанных линейных моделей в целом согласуются с результатами дисперсионного анализа с усреднением по испытуемым. Однако у смешанных моделей есть ряд преимуществ. В частности, они позволяют проверить предположение о необходимости учета тех или иных случайных факторов (в рассмотренном случае фактор стимула оказался излишним) и получить данные о взаимосвязях между случайными факторами, что позволило показать негативную корреляцию между отклонением времени неправильных ответов испытуемого от среднего времени неправильных ответов и отклонением от среднего разницы по времени между правильными и неправильными ответами. Чем медленнее ошибочные ответы испытуемых, тем меньше различие по времени правильных и неправильных ответов, то есть тем слабее эффект замедления на ошибочных ответах. Кроме того, поскольку в смешанных моделях в явном виде учитываются возможные источники искажения в данных, это позволяет заранее отвергнуть критику, связанную с этими источниками, возможную в случае дисперсионного анализа сырых данных. Таким образом, в описанном случае смешанная модель не показывает различий с дисперсионным анализом в результатах статистических тестов для отдельных факторов, однако позволяет с большей уверенностью делать выводы о результатах исследования. Кроме того, необходимо помнить, что априорных оснований предпочитать анализ «по стимулам» анализу «по испытуемым» нет, хотя мы с тем же успехом могли получить ситуацию, когда бы сильное влияние оказывал фактор стимула, а не фактор испытуемого. В этом случае анализ «по испытуемым» дал бы ошибочные результаты. Исходя из этого, использование смешанных моделей с точки зрения автора оказывается вполне целесообразным — в худшем случае они покажут те же результаты, что и дисперсионный анализ, а в лучшем позволят избежать грубых ошибок.
Применение смешанной регрессии оставляет исследователю значительно больше свободы в выборе эффектов для включения в модель. При этом в случае простых моделей, где случайные эффекты сгруппированы только по одной переменной (например, по испытуемым), рекомендуется включать в случайные эффекты все те переменные, которые используются среди фиксированных эффектов и для которых есть повторные измерения. Например, если речь идет об обычном внутригрупповом плане 2x2, то обе независимые переменные и их взаимодействие должны быть включены в модель как в качестве фиксированных, так и в качестве случайных эффектов с группировкой по испытуемым. В противном случае увеличивается вероятность ложнопозитивных результатов (Barr et al., 2013). Однако когда речь идет о более сложных моделях, то возникает ряд затруднений. При увеличении числа случай
ных эффектов растет время расчетов и вероятность проблем подгонки моделей. Рекомендация автора — исходить из теоретических представлений о том, какие факторы будут оказывать влияние, и использовать один и тот же подход для всей серии исследований. Может возникнуть впечатление, что подобные рекомендации оставляют слишком большой простор для манипуляций. Однако нужно помнить, что проблема выбора модели характерна не только для регрессии со смешанными эффектами. Например, дисперсионный анализ также позволяет включать в модель дополнительные предикторы (например, пол испытуемого, возраст, среднее время ответа, номер пробы и т. д.). Регрессионный подход всего лишь делает эту проблему явной, вынуждая исследователя задумываться о предпосылках, лежащих в основе его действий. Наконец, один статистический результат сам по себе не подтверждает и не опровергает теоретическую гипотезу. Только серия исследований может позволить сделать это, а в таком случае модель, произвольно подогнанная ради получения заветной значимости в одном исследовании, вряд ли покажет тот же результат в другом исследовании.
Литература
Королькова О. А. Перцептивное пространство и предикторы различения эмоциональных экспрессий лица // Российский журнал когнитивной науки. 2014. Т. 1. №4. С. 82-97. URL: http://cogjournal.Org/l/4/pdf/KorolkovaRTCS2014b.pdf.
Bakker М., Wicherts J.M. The (mis)reporting of statistical results in psychology journals 11 Behavior Research Methods. 2011. Vol. 43. No.3. P. 666-678. doi:10.3758/sl3428-0U-0089-5
Baldwins. A., BerkeljonA., Atkins D.C., Olsen J. A., Nielsen S. L. Rates of change in naturalistic psychotherapy: Contrasting dose-effect and good-enough level models of change // Journal of Consulting and Clinical Psychology. 2009. Vol. 77. No.2. P. 203-211. doi:10.1037/a0015235
Barr D. J, Levy R., Scheepers C., TilyH.J. Random effects structure for confirmatory hypothesis testing: Keep it maximal // Journal of Memory and Language. 2013. Vol. 68. No.3. P. 255-278. doi: 10.1016/j.jml.2012.11.001
Bates D. [R] Imer, p-values and all that // R-help mailing list. 2006. URL: https://stat.ethz.ch/pipermail/r-help/2006- May7094765.html.
Bates D., Maechler M., Bolker B., Walker S. Ime4: Linear mixed-effects models using Eigen and 84 2014. URL: http:// cran.r-project.org/package-lme4
Biesanz J. C., Human L. J. The cost of forming more accurate impressions: accuracy-motivated perceivers see the personality of others more distinctively but less normatively than perceivers without an explicit goal // Psychological Science. 2010. Vol. 21. No.4. P. 589-594. doi:10.U77/0956797610364121
Chetverikov A. Warmth of familiarity and chill of error: Affective consequences of recognition decisions // Cognition & Emotion. 2014. Vol. 28. No.3. P. 385-415. doi:10.1080/02699931 .2013.833085
Clark H.H. The language-as-fbced-effect fallacy: A critique of language statistics in psychological research // Journal of Verbal Learning and Verbal Behavior. 1973. Vol. 12. P. 335-359. doi: 10.1016/80022-5371(73)80014-3
Gelman A. Analysis of variance: Why it is more important than ever // The Annals of Statistics. 2005. Vol. 33. No. 1. P. 1-53. doi: 10.1214/009053604000001048
Gelman A., Hill J. Data analysis using regression and multi- level/hierarchical models. New York, USA: Cambridge Univ Press, 2007.
GLMM package comparison 2015. URL: http://glmm.wikidot.com/pkg-comparison
Gulbinaite R., Johnson A., de Jong R., Morey C. C, van Rijn H. Dissociable mechanisms underlying individual differences in visual working memory capacity // NeuroImage. 2014. Vol. 99. P. 197-206. doi:10.1016/j.neuroimage.2014.05.060
Halekoh U., Hojsgaard S. A Kenward-Roger approximation and parametric bootstrap methods for tests in linear mixed models - The R package pbkrtest // Journal of Statistical Software. 2014. Vol. 59. No. 9. P. 1-30. URL: http://www.jstatsoft.org/v59/І09/
Jaeger T. F. Categorical data analysis: Away from ANOVAs (transformation or not) and towards Logit Mixed Models // Journal of Memory and Language. 2008. Vol. 59. No. 4. P. 434-446. doi: 10.1016/j.jml.2007.11.007
Jara A., Hanson T., Quintana F, Müller P., Rosner G. DPpackage: Bayesian semi- and nonparametric modeling in R11 Journal of Statistical Software. 2011. Vol. 40. No. 5. P. 1-30. URL: http://www.jstatsoft.org/v40/i05/.
Kristjänsson Ami Johannesson Ö. I. How priming in visual search affects response time distributions: Analyses with exGaussian fits // Attention, Perception & Psychophysics. 2014. Vol. 76. No.8. P. 2199-2211. doi:10.3758/sl3414-014-0735-y
Kuznetsova A., BrockhoffP. B., Christensen R. HB. ImerTest: Tests in Linear Mixed Effects Models 2014. URL: http://cran.r- project.org/package-lmerTest.
Laubrock J, Engbert R., Kliegl R. Taxational eye movements predict the perceived direction of ambiguous apparent motion // Journal of Vision. 2008. Vol. 8. No. 14. P. 13.1-13.17. doi: 10.1167/8.14,13
Mousikou P, Kinoshita S., Wu S., Norris D. Transposed- letter priming effects in reading aloud words and nonwords // Psychonomic Bulletin & Review. 2015. Vol. Online first. P. 1-6. doi: 10.3758/sl3423-015-0806-7
Oberauer К., Kliegl R. A formal model of capacity limits in working memory // Journal of Memory and Language. 2006. Vol. 55. P. 601-626. doi:10.1016/j.jml.2006.08.009
Pinheiro J. C., Bates D. M. Mixed effects models in S and S-Plus. NewYork: Springer Verlag, 2000. doi:10.1198/tech.2Q01. s574
R Core Team R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing, 2014. URL: http://www.r-project.org/.
RaaijmakersJ. G.W A further look at the “language-as- fbced-effect fallacy” // Canadian Journal of Experimental Psychology. 2003. Vol. 57. No.3. P. 141-151. URL: http://www.ncbi.nlm.nih.gov/pubmed/14596473
Raaijmakers J. G.W, Schrijnemakers J.M.C., Gremmen F. How to deal with “the language-as-fbced-effect fallacy”: Common misconceptions and alternative solutions // Journal of Memory and Language. 1999. Vol. 41. No. 3. P. 416-426.
r-sig-mixed-models FAQ-GLMM 2015. URL: http://glmm.wikidot.com/faq
Sandberg K., Timmermans B., OvergaardM., CleeremansA. Measuring consciousness: is one measure better than the other? // Consciousness and Cognition. 2010. Vol. 19. No. 4. P. 1069-1078. doi: 10.1016/j.concog.2009.12.013
Sarkar D., DebRoy S., Bates D., Pinheiro J, the R Core team nlme: Linear and nonlinear mixed effects models // R package version 3.1-90. R package version 3.1-90, 2008.
Wright D. B., London K. Multilevel modelling: Beyond the basic applications // The British Journal of Mathematical and Statistical Psychology. 2009. Vol. 62. No.Pt 2. P. 439-456. doi: 10.1348/000711008X327632
Wright D. B., London K., Waechter M. Social anxiety moderates memory conformity in adolescents // Applied Cognitive Psychology. 2010. Vol. 24. No. 7. P. 1034-1045. doi:10.1002/acp
Wu Y., Clark L. Disappointment and regret enhance cor- rugator reactivity in a gambling task // Psychophysiology. 2014. Vol. 52. No.4. P. 518-523. doi:10.1111/psyp.l2371





