Цель данного сообщения — определить на двумерной сфере S² дифференцируемый гомеоморфизм, который, будучи структурно устойчивым в смысле Андронова–Понтрягина [1] вместе с тем имеет периодические точки сколь угодно больших периодов и не локально связное минимальное множество.

Согласно [2], это отвечает на вопрос, поставленный Андроновым (можно рассмотреть индуцированный поток на S²×S¹).

Напомним определение структурной устойчивости. Два дифференцируемых (C^∞) гомеоморфизма T, T¹ замкнутого C^∞ многообразиям называются эквивалентными, если существует гомеоморфизм h : M → M такой, что hT = T¹h. Они называются ε-эквивалентными, если гомеоморфизм h можно выбрать так, чтобы он отличался (в любой точке) от тождественного отображения менее, чем на ε. Пусть d₁– это C¹-метрика на пространстве τm дифференцируемых гомеоморфизмов многообразия M. Тогда T ∈ τm называется структурно устойчивым, если для любого ε > 0 существует δ > 0 такое, что все T¹ ∈ τm, удовлетворяющие неравенству d1(T,T¹) < δ, ε-эквиваленитны T.

Теперь мы опишем дифференцируемый гомеоморфизм T : S² → S² со свойствами, указанными выше. Для удобства мы задаём T на плоскости E², понимая E² как S² \ p, где Tp = p

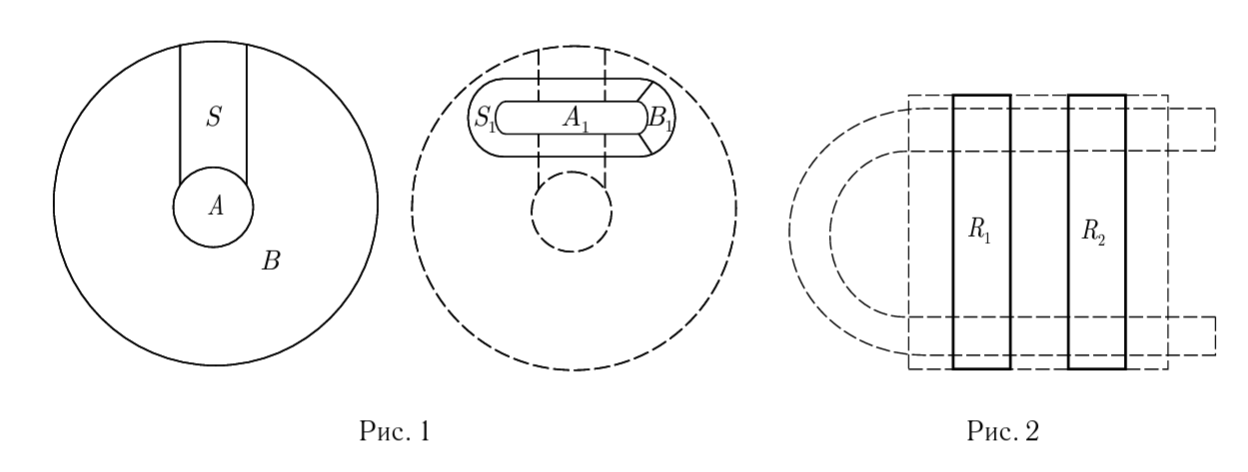
Дифференцируемый гомеоморфизм T преобразует области, как показано на рис. 1 (B → B₁ и т.д.), и, кроме того, он удовлетворяет следующим условиям:

a) Матрица Якоби отображения T имеет собственные числа, по модулю меньшие единицы, на внешней части множества T⁻¹(внешняя граница B) и на B₁

b) T⁻¹(S∩S₁)представляет собой два вертикальных прямоугольника R₁,R₂ вS (как показано на рис. 2), и на каждом из этих прямоугольников отображение T является «почти» линейным: оно достаточно близко в C¹-смысле к линейному отображению на R₁,R₂.

Теперь можно построить естественное взаимно-однозначное соответствие между точками множества K = ∩∞m=_−∞T^m(S) и совокупностью всех бесконечных в обе стороны последовательностей из единичек и двоек с фиксированным положением «десятичной запятой»: . . . 1211, 21112... и т.д. При этом периодическим точкам в K соответствуют периодические последовательности. Исходя из указанного описания, можно получить нормальную форму для T и использовать её для построения гомеоморфизма, приведённого в данном примере.

Список литературы

[1] Андронов, А.А., Понтрягин, Л.С., Грубые системы, Докл. АН СССР, т. 14, №5, 1937, с. 247–250.

[2] Markus, L., On the behaviour of the Solutions of a Differential System Near a Periodic Solution, with Applications to the Theory of Structurally Stable Systems, Technical Report 8, O O R project 1469, University of Minnesota, 1959