Основной тезис статьи А. Л. Крушинского заключается в том, что «за решение логической задачи надо заплатить увеличением энтропии мозга». К этому утверждению автор подводит читателя, прослеживая основные исторические вехи в разрешении вопроса о связи между термодинамической энтропией и информацией. Принятие этого тезиса означает, что необходимым условием функционирования мозга является его «высокая упорядоченность», которую автор, следуя Л.В.Крушинскому, связывает с избыточным числом нейронов,и постепенной потерей которой мозг оплачивает получение и создание информации. Следствия заявленного принципа для теории эволюции иллюстрируются в статье на ряде примеров.

Неудивительно, что работа, затрагивающая столь широкий круг вопросов и опирающаяся на столь широкий круг научных дисциплин — от статистической физики и биофизики до теории эволюции и когнитивной науки, поневоле носит конспективный характер. Однако общее впечатление, возникающее при знакомстве с этой работой, можно, пожалуй, выразить так: автор рисует слишком уж благостную картину, в которой все положения представляются стоящими на фундаменте твердо установленных фактов. Между тем такова ли эта картина в реальности? И главное — автор, как мне представляется, не привел весомых аргументов в пользу своего главного тезиса, в то время как изложение связи между термодинамической и информационной энтропией можно найти в учебниках. Остается неясным, почему именно мозг должен расплачиваться за решение задачи. Возможно, для автора было вполне очевидным по каким-то причинам, однако я этих причин не увидел и не уверен, что их увидят и другие читатели. Ниже я коснусь некоторых вопросов, которые, как мне представляется, имеют непосредственное отношение к основному тезису статьи, сохраняя при этом принятую А. Л. Крушинским несколько антропоморфную терминологию («логические задачи» и «рассудочная деятельность»),

1. Порядок и хаос в открытых системах, далеких от термодинамического равновесия

К основному тезису работы А.Л Крушинский подводит читателя с помощью последовательности следующих логических шагов. Энтропия характеризует степень «беспорядка» в системе, а негэнтропия (энтропия, взятая с противоположным знаком) характеризует степень «упорядоченности» системы. Делается допущение, что информация эквивалентна негэнтро- пии. Согласно второму началу термодинамики, энтропия замкнутой системы не может убывать. Получение информации организмом эквивалентно уменьшению энтропии в подсистеме «организм» и оно оплачивается ростом энтропии во внешней среде, так чтобы суммарная энтропия системы «организм + внешняя среда» не уменьшалась бы. Однако с точки зрения этой последовательности вывод, к которому приходит автор работы, выглядит несколько неожиданно: выходит, что получение живым организмом информации о закономерностях внешней среды и «мыслительный процесс» увеличивают энтропию именно мозга, а не внешней среды, как, казалось бы, следует из предыдущих логических построений. Все выглядит так, как будто негэнтропия нарастает не в ЦНС, а где-то в «уме» или «душе», по отношению к которым мозг почему-то выступает в качестве «внешней среды».

Рассмотрим спонтанное возникновение упорядоченной структуры в жидкости, находящейся в неравновесных условиях — пример, который использует Германн Хакен (1991), иллюстрируя процессы самоорганизации. Если плоскую кювету с маслом равномерно подогревать снизу, при определенной температуре помимо хаотического теплового движения молекул в масле возникает макроскопически упорядоченная структура — конвекционные ячейки, напоминающие пчелиные соты. В этом примере мы имеем очевидный случай упорядочивания системы (масла). Куда делся избыток энтропии? Ответ очевиден: увеличилась энтропия окружающей среды. Почему же, говоря о мозге, мы должны рассуждать по-другому и полагать, что в случае получения им (или создания в нем) новой информации избыток энтропии должен непременно уменьшать степень его упорядоченности?

Соотношение между информационной и термодинамической энтропией, на которое опирался А. Л. Крушинский, получено в рамках термодинамики равновесных систем. Насколько оправдан такой подход применительно к мозгу? В живом функционирующем мозге (автор справедливо отмечает, что мозг представляет собой открытую и далекую от термодинамического равновесия систему) можно выделить различные степени свободы: колебательные и вращательные степени свободы свободных молекул в жидких фракциях, колебательные степени свободы в молекулах в связанном состоянии, определенные конфигурации нейронов, связанных в сети и т.п. Достижение организмом теплового (термодинамического) равновесия означало бы, что энергия равномерно распределена по этим степеням свободы. Так ли это на самом деле? На уровне отдельного нейрона мы наблюдаем резкие градиенты концентраций ионов (достаточно вспомнить здесь натриево-калиевый насос, поддерживающий трансмембранный потенциал покоя в нейроне). Происходит активный обмен не только энергией, но и массой с внешней для мозга средой (синтез белков). Среди прочего можно выделить степени свободы, связанные с биоэлектрическими явлениями. Как бы выглядели электрические явления в мозге, находящемся в состоянии термодинамического равновесия? Они выродились бы в спонтанные флуктуации. Вместо этого мы наблюдаем отчетливую упорядоченность биоэлектрических процессов, проявляющуюся даже в том случае, когда мы имеем дело с суммарными потенциалами, регистрируемыми с поверхности головы (ЭЭГ). Таким образом, различные уровни (молекулярный, клеточный, системный) не находятся в состоянии теплового равновесия, и обмен между ними протекает со скоростями, определяемыми структурными особенностями этих уровней.

С точки зрения обсуждаемого вопроса особый смысл приобретает одно замечание Л. А. Блюменфель- да (1977). Разбирая пример со свободными нуклеотидами, объединяющимися в биополимерную структуру, он отмечает, что принципиальное значение для биологических систем приобретает понятие конструкции. Возникновение конструкций — устойчивых долгоживущих агрегаций — связывает ранее независимые степени свободы и радикальным образом меняет число микроскопических состояний и их вероятности, а также характерное время возврата в равновесное состояние (время релаксации) и тем самым — оценку упорядоченности биологической системы.

Кроме того, вопрос о соотношении термодинамической и информационной энтропии отнюдь не является тривиальным. Г. Хакен (1991) отмечает два существенных свойства Шенноновской информации: 1) она никак не учитывает смысл сигнала и 2) относится к замкнутым системам, то есть предполагает заданный набор («алфавит») сигналов.

Г. Хакен (1991) рассматривает существенно нелинейные динамические системы вида

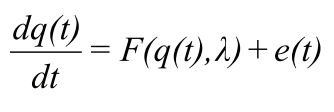
которые описывают эволюцию вектора состояния системы q(t). Сигнал (например, сенсорный сигнал, несущий информацию о внешнем мире) воздействует на такую динамическую систему посредством изменения параметра Ä.. К моменту прихода сигнала система уже обладает некоторым набором динамически устойчивых состояний — аттракторов. Внешнее воздействие может создавать новые аттракторы, присутствие стохастической части — шума e(t) — позволяет системе непредсказуемо переходить к одному из множества аттракторов, то есть фактически изменять вероятности микросостояний системы (нарушение предположения о равной вероятности всех микроскопических состояний, на котором основана формула Больцмана).

Один из полученных Г. Хакеном результатов заключается в том, что в системе, далекой от термодинамического равновесия, энтропия может возрастать, несмотря на то, что эта система переходит в более упорядоченное состояние. Что в этом случае следует думать об энтропийной плате за возникновение порядка? Основной тезис А. Л. Крушинского, по крайней мере по первому впечатлению, находится в явном противоречии с этим результатом.

Боле того, для того чтобы учесть осмысленность (значимость) сигнала, Хакен вводит понятие относительной значимости, и в формуле Шеннона у него фигурируют не вероятности, а величины относительной значимости. С одной стороны, при таком подходе создание нового аттрактора становится возможным понимать как возникновение смысла, «самозарождение» смысла. С другой стороны, отказ от использования вероятности микроскопических состояний в формуле Шеннона делает менее очевидной связь полученной меры с термодинамической энтропией.

2. Онтогенез и информационная энтропия

Развитие организма начинается с одной клетки. Человеческое тело содержит примерно ІО¹⁴ клеток, из которых примерно ІО¹⁰ образуют мозг. В какой момент происходит формирование того изначального и растрачиваемого в процессе последующей рассудочной деятельности запаса упорядоченности, о котором говорит А. Л. Крушинский? В онтогенезе мозг человека претерпевает грандиозные структурные изменения. До четырехмесячного возраста происходят запрограммированная гибель нейронов и, одновременно с этим, синаптогенез, который сменяется синаптическим пру- нингом (удалением «лишних» синапсов), продолжающимся в течение всего жизненного пути человека. Миелинизация, дендритная и аксонная арборизация происходят фактически на протяжении всего жизненного цикла человека (Lenroot, Giedd, 2006). Не следует забывать также, что и во взрослом состоянии (в том числе и у человека) происходит рождение новых нейронов (Eriksson et al., 1998; Ernst et al., 2014). На фоне этих процессов от младенчества до конца жизни происходит рассудочная деятельность. На всех ли этапах она сопровождается потерей упорядоченности мозга? Все эти процессы должны быть как-то учтены при количественной оценке степени упорядоченности мозга.

3. Избыточность как излишек и как достаточный запас

Говоря об избыточности, А. Л. Крушинский отмечает, что им «используется общепринятое представление об избыточности как о наличии большего количества нейронов, чем то, которое могло бы обеспечить нормальное функционирование организма» (с. 53). Оставив в стороне вопрос о том, насколько такое определение можно считать «общепринятым» (об этом чуть ниже), отмечу, что понятие избыточности является относительным. Можно оценивать избыточность структурной организации мозга по отношению к определенному кругу задач, к определенной ситуации. Так, «ситуативно-избыточным» является опорно-двигательный аппарат. В частности, кинематические цепи руки обладают существенно большим числом степеней свободы (более 30), чем это необходимо для выполнения движений, составляющих двигательный типичный репертуар человека.

Для обоснования тезиса об избыточности автор статьи приводит результаты опытов на животных. Мне представляется, что опыты на животных иллюстрируют именно ситуативную структурную избыточность мозга, поскольку в экспериментах с неизбежностью исследуются лишь вполне определенные аспекты поведения, показывающие отсутствие влияния разрушения части мозга на наблюдаемые функции. Между тем, с точки зрения жизненного пути организма, то, что представляется избыточным ситуативно, может оказаться необходимым условием развития и адаптивного поведения. С позиций нейро-дарвинизма (Sporns, Edelman, 1993; Hadders-Algra, 2000, 2010) наличие подобной ситуативной избыточности является необходимым условием развития — отбора «полезных» нейронных конфигураций и образования связей между ними. С точки зрения филогенеза, индивидуальная избыточность, приводящая к внутривидовому разнообразию, может оказаться необходимой для эволюционной судьбы рода.

Таким образом, пониманию термина «избыточность» в смысле чего-то излишнего, на что явно указывает принятое А. Л. Крушинским определение избыточности, можно, следуя И. М. Гельфанду и М. Л. Латашу (1998), противопоставить понимание этого термина в смысле наличия достаточного запаса. В английском языке этим двум оттенкам смысла соответствуют два слова — redundancy и abundance.

4. Об информационной природе логических (когнитивных) операций

В статье утверждается, что «Минимальное количество энергии, требуемое на получение одного бита, определяется по формуле: E = TAS = Tkln2 (12)» (с. 55). Между тем обсуждать энтропийную плату за решение логической задачи, не вдаваясь при этом в характер самих логических операций, представляется интуитивно не вполне оправданным. Много ли мы знаем о природе этих операций? Оправдано ли рассматривать все эти операции как имеющие одну природу? Поясню этот вопрос: ряд исследований показывает, что, как минимум, следует различать логически необратимые и обратимые процессы преобразования информации. В соответствии с принципом Ландауера (Landauer, 1961), энергетическая плата в виде диссипации тепловой энергии составляет kTln2 Дж/бит, но относится исключительно к необратимым преобразованиям информации. Этому, как следует из соотношения (12), очевидно, соответствует и «энтропийная плата»: ΔS=ΔQ/T Недавно была выполнена экспериментальная работа (Orlov et al., 2012), которая подтвердила существенное различие между необратимыми и обратимыми преобразованиями информации. Оказалось, что в случае необратимого преобразования информации диссипация энергии в пересчете на один бит существенно превосходит теоретический нижний предел kTln2, в то время как осуществление обратимого преобразования практически не сопровождается рассеянием тепла, и в этом смысле, как отмечают авторы этого исследования, «there is no fundamental lower limit to the amount of energy dissipation required to move information from place to place. Communication is in this sense fundamentally free» (стр. 06FE10-5). Существуют ли обратимые и необратимые когнитивные процессы? Если да, то их следует различать, и энтропийная плата, очевидно, будет зависеть от соотношения тех и других.

Возникает и ряд других вопросов. Что является результатом решения логической задачи? Всегда ли это решение является созданием новой информации? Рассмотрим простейший пример: некто хранил в своей памяти N фактов, по видимости не связанных друг с другом. В результате рассудочной деятельности им была установлена причинная связь между ними, и все N фактов оказались следствиями давно известного рассуждающему субъекту закона. Следует ли полагать, что в этом случае результатом рассудочной деятельности было создание новой информации? Не следует ли считать, что исчезновение N самостоятельных фактов означает исчезновение информации? Каков итоговый баланс между приобретением и потерей информации?

Справедливости ради следует отметить, что автор отмечает, насколько сложен вопрос, в примечании: «По мнению М. В. Волькенштейна (2008), биологические системы в процессе эволюции приближаются к состоянию, в котором они “платят” по кТ1п2 за один бит ценной информации и не “платят” ничего за невоспринимаемую информацию, не обладающую ценностью. В принципе, разделяя эту точку зрения, добавлю, что вопрос о ценности информации достаточно сложен и неоднозначен» (с. 55).

Литература

Бпюменфепьд Л. А. Проблемы биологической физики. Изд. 2-е, испр. и доп. М.: Главная редакция физико-математической литературы изд-ва «Наука», 1977.

Хакен Г. Информация и самоорганизация: Макроскопический подход к сложным системам. М.: Мир, 1991.

Eriksson Р. S., Perfilieva Е., Björk-Eriksson Т., Alborn А.-М., Nordborg С., Peterson D. A., Gage ЕН. Neurogenesis in the adult human hippocampus // Nature Medicine. 1998. Vol. 4. No. 11. P. 1313-1317. doi:10.1038/3305

Ernst A., Alkass K., Bernard S., Salehpour M., Perl S., Tisdale J., Possnert G., Druid H, Frisen J. Neurogenesis in the striatum of the adult human brain // Cell. 2014. Vol. 156. No. 5. P. 1072-1083. doi:10.1016/j.cell.2014.01.044

Gelfand I. M., Latash M. L. On the problem of adequate language in motor control 11 Motor Control. 1998. Vol. 2. No. 4. P. 306-313.

Hadders-Algra M. The neuronal group selection theory: a framework to explain variation in normal motor development 11 Developmental Medicine & Child Neurology. 2000. Vol. 42. No. 8. P. 566-572. doi:10.1017/S0012162200001067

Hadders-Algra M. Variation and variability: key words in human motor development // Physical Therapy. 2010. Vol. 90. No. 12. P. 1823-1837. doi:10.2522/ptj.20100006

Landauer R. Irreversibility and heat generation in the computing process 11 IBM Journal of Research and Development. 1961. Vol. 5. No.3.P. 183-191.

Lenroot R. K., Giedd J. N. Brain development in children and adolescents: insights from anatomical magnetic resonance imaging 11 Neuroscience & Biobehavioral Reviews. 2006. Vol. 30. No. 6. P. 718-729. doi:10.1016/j.neubiorev.2006.06.001

Orlov A. O., Lent C. S., Thorpe С. C., Boechler G. R, Snider G. L. Experimental test of Landauer's Principle at the sub-kBT level 11 Japanese Journal of Applied Physics. 2012. Vol. 51. No. 68. P. 06FE10. doi:10.1143/TTAP.51.06FE10

Sporns O., Edelman G.M. Solving Bernstein's problem: A proposal for the development of coordinated movement by selection 11 Child Development. 1993. Vol. 64. No. 4. P. 960-981. doi:10.2307/1131321

Вместо заключения

Настоящие заметки оформились в результате рецензирования первого варианта статьи А. Л. Крушинско- го, направленного в редакцию «Российского журнала когнитивной науки». Лишь позже я с прискорбием узнал, что Алексея Леонидовича Крушинского уже нет с нами. Найти общий объяснительный принцип, увидеть простое в сложном — это извечная потребность человеческого ума. Именно к этому стремился Алексей Леонидович, и его попытка не прошла даром — она вызвала к жизни научную дискуссию.