Пространственные взаимодействия: оценка на основе глобального и локального индексов Морана


Published: Oct. 1, 2014
Latest article update: Nov. 29, 2022
Abstract
В настоящей работе авторы демонстрируют возможности использования глобального и локального индексов Морана на примере Самарской области. В исследовании за единицы территорий (районов) взяты 37 муниципальных образований 1-го уровня - 10 городских округов и 27 муниципальных районов. На основе глобального индекса Морана построена пространственная диаграмма рассеяния, выявлены четыре территоральных кластера. Далее с помощью локального индекса Морана были определены шесть подкластеров. Разложение локального индекса на составляющие позволило выявить как зоны влияния для каждого конкретного ядра (на примере Самарского), так и зоны совместного влияния нескольких ядер (на примере объединенной системы Самара - Тольятти).
Keywords
Кластер, глобальный индекс Морана, Самарская область, локальный индекс Морана, Пространственная автокорреляция
Оценка пространственных взаимодействий экономических систем, учет пространственной компоненты являются необходимым элементом современных экономических исследований. Результативность исследований определяется используемым инструментарием. Наиболее эфективными для целей пространственного анализа являются методы пространственной эконометрики [5; 8; 12; 14; 16]. Для выявления пространственных взаимодействий широко используется глобальный и локальный индексы Морана, на основе которых определяются пространственные кластеры и их характеристики. В настоящей работе авторы демонстрируют возможности использования индексов на примере Самарской области. Алгоритм оценки силы взаимовлияния территорий и их кластеризации представлен на рисунке 1.
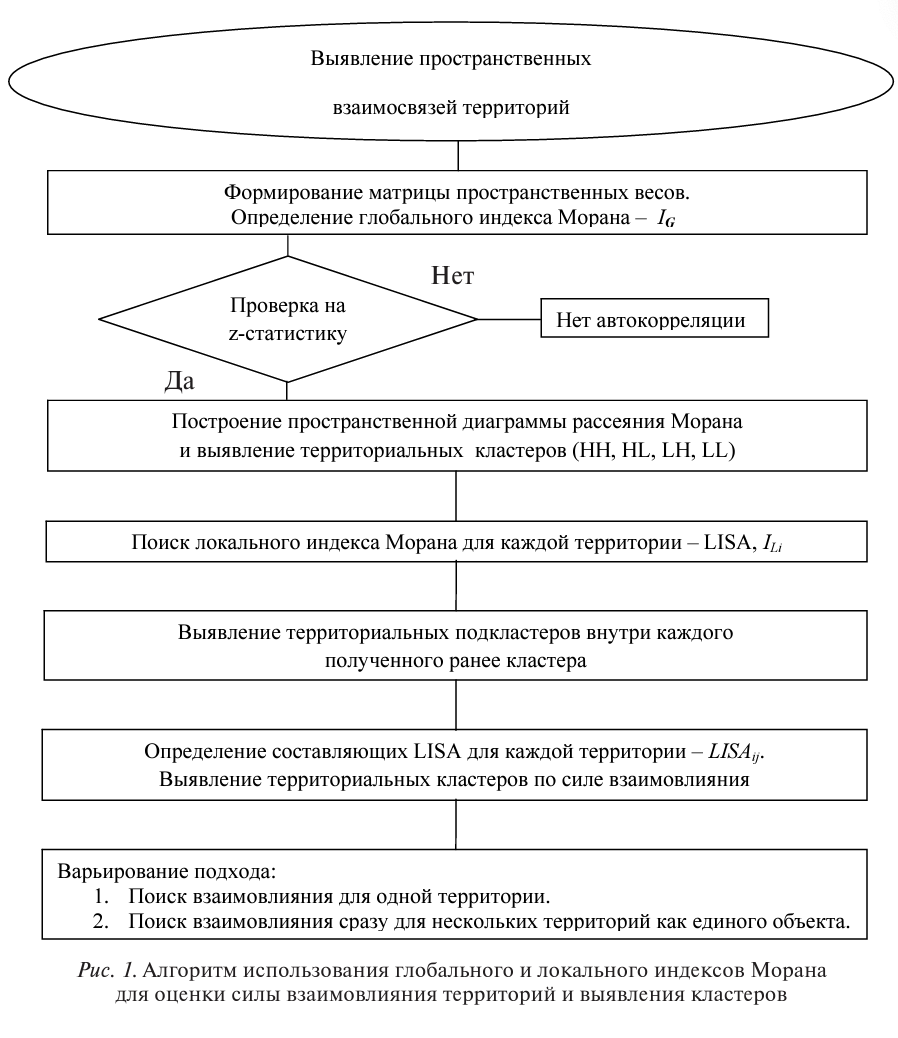
МЕТОДОЛОГИЯ ИССЛЕДОВАНИЯ
Объект, статистическая база и инструментарий
В исследовании за единицы территорий (районов) взяты 37 муниципальных образований 1-го уровня - 10 городских округов и 27 муниципальных районов Самарской области.
В качестве источника данных по территориям выступил официальный сайт Федеральной службы государственной статистики [9]; данных по дистанции-расстоянию - сайты [1; 2].
В качестве матрицы пространственных весов используем матрицу расстояний (правильнее было бы использовать экономическое расстояние, выраженное в изохронах, однако первичные результаты исследования показали, что этот метод менее удачен по сравнению с использованием географического расстояния). Расстояние определяется от центров территорий [3; 7]. При совпадении центров различных территорий (например, г. о. Сызрань и Сызранского района) используем минимальное возможное значение (например, «1») [17].
Обработка данных осуществлялась с использованием надстройки для Excel - statistiXL [11].
Гипотеза о значимости индексов Морана проверяется традиционным способом с использованием z-статистики.
Глобальный индекс Морана определяется по формуле:

Важным этапом анализа полученных данных является построение пространственной диаграммы рассеяния Морана. По оси абсцисс откладываются стандартизированные £-значения исследуемого показателя, а по оси ординат - значения пространственного фактора Wz. На диаграмме отображается линия регрессии Wz на наклон который равен коэффициенту общей пространственной автокорреляции Iпри стандартизированной матрице весов [5].
Коэффициент пространственной автокорреляции показывает степень линейной взаимосвязи между вектором £ центрированных значений исследуемого показателя и вектором Wz пространственно взвешенных центрированных значений исследуемого показателя в соседних территориях (районах), который называется пространственным лагом (Spatially lagged vector) [5].
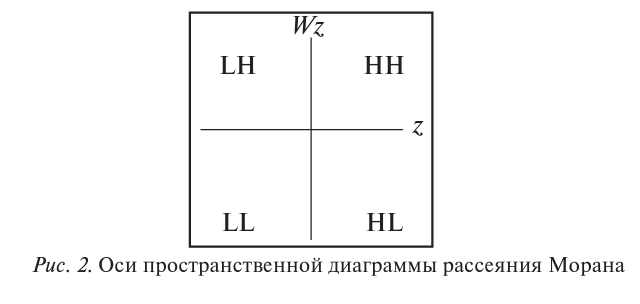
Оси пространственной диаграммы рассеяния Морана представлены на рисунке 2.
Квадрант НН - территории в нем имеют относительно высокие собственные значения анализируемого показателя, окружены территориями также с
относительно высокими значениями анализируемого показателя. Автокорреляция положительная.
Квадрант LL - территории в нем имеют относительно низкие собственные значения анализируемого показателя, окружены территориями также с относительно низкими значениями анализируемого показателя. Автокорреляция положительная.
Квадрант HL - территории в нем имеют относительно высокие собственные значения анализируемого показателя, окружены территориями с относительно низкими значениями анализируемого показателя. Автокорреляция отрицательная.
Квадрант LH - территории в нем имеют относительно низкие собственные значения анализируемого показателя, окружены территориями с относительно высокими значениями анализируемого показателя. Автокорреляция отрицательная.
Стоит также отметить, что расчет характеристик пространстве иной корреляции является лишь предварительным этапом пространственного эконометрического анализа. Указанные характеристики свидетельствуют о наличии, но не объясняют причин кластеризации территорий в пространстве.
Локальный индекс Морана (LISA - Local Index Spatial Autocorrelation) вычисляется no формуле [9; 12; 13; 17]:

Матричные методы расчета составляющих локального индекса Морана
В процессе исследования характеристик взаимовлияния изучаемой территории (территорий) и всех ближних или дальних ее (их) соседей возможно вести поиск для:
а) любой территории в отдельности;
б) совокупности территорий, объединенных по одному критерию (например, для каждого ядра в отдельности, для совокупности ядер при изучении влияния на территорию Самарской области) - для территориальных кластеров (подкластеров как составляющих кластеров) и всей совокупности территорий (районов);
в) совокупности территорий, объединенных сразу по нескольким критериям (например, сначала выявляем ядра, затем выявляем силу взаимосвязей для совокупной системы ядер, затем выявляем взаимозависимости уже для наиболее «зависимых» поясов влияния и т. д., т. е. по «нарастающему итогу»).
Исходной посылкой такого утверждения является анализ математических действий, выполняемых при определении локального индекса Морана. Результатом одного из действий является матрица составляющих LISA по каждой территории. При этом немаловажно, что в ней уже учтен эффект автокорреляции. Полагаем, что указанные составляющие выступают не только в качестве промежуточных результатов, но могут быть равноценно использованы в целях углубленного анализа взаимосвязей по каждой отдельной территории. Следовательно, помимо глобального и локального (LISA) индексов Морана, возможно выявить составляющие LISA по каждой территории, т. е. охарактеризовать силу взаимовлияния территории (района) по отношению ко всем ближним или дальним территориям-соседям.
Последовательность действий по поиску составляющих LISA:
- Стандартизация данных искомого показателя (численности населения):

где zi - стандартизированные значения; Serror (х) - стандартное отклонение по всем территориям.
- Стандартизация дистанции:
- строим матрицу фактических дистанций между территориями (хij);
- строим относительную матрицу дистанций между территориями Vij:

где Vij - относительная дистанция от одной территории до другой; х - фактические данные по дистанции между двумя территориями.
Ищем совокупность всех Vij.

Определяем стандартизированную дистанцию W [14].

где Wij - стандартизованная дистанция между двумя территориями.

- В результате указанных расчетов получаем матрицу силы взаимовлияния территорий (районов) друг на друга, с уже учтенным эффектом автокорреляции:

где LISAij - сила взаимовлияния между двумя конкретными территориями.
Использование индексов Морана предполагает как прямое, так и обратное движение [15]. Сумма составляющих по каждой территории представляет собой не что иное, как сам локальный индекс Морана (LISA). А сумма всех LISA составляет глобальный индекс Морана.
Таким образом, LISA можно определить двумя способами:
- по формуле (2);
- в качестве промежуточного действия при расчете глобального индекса Морана (9):
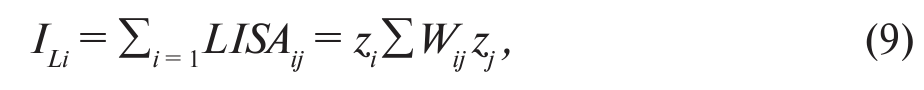
где Iij. - локальный индекс Морана для конкретной территории і. Он равен сумме всех составляющих LISA с участием изучаемой нами территории і.
Таким образом, руководствуемся следующим принципом: не суммируем все LISAij, а выбираем из них только значения с участием изучаемой территории и при этом избегаем двойного счета.
Определение глобального индекса Морана:
IG = ∑ILi .
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ ДЛЯ ТЕРРИТОРИЙ САМАРСКОЙ ОБЛАСТИ (2012 г.)
Глобальный индекс Морана
Результаты расчетов для построения пространственной диаграммы рассеяния Морана для территорий Самарской области представлены в таблице.
ICC
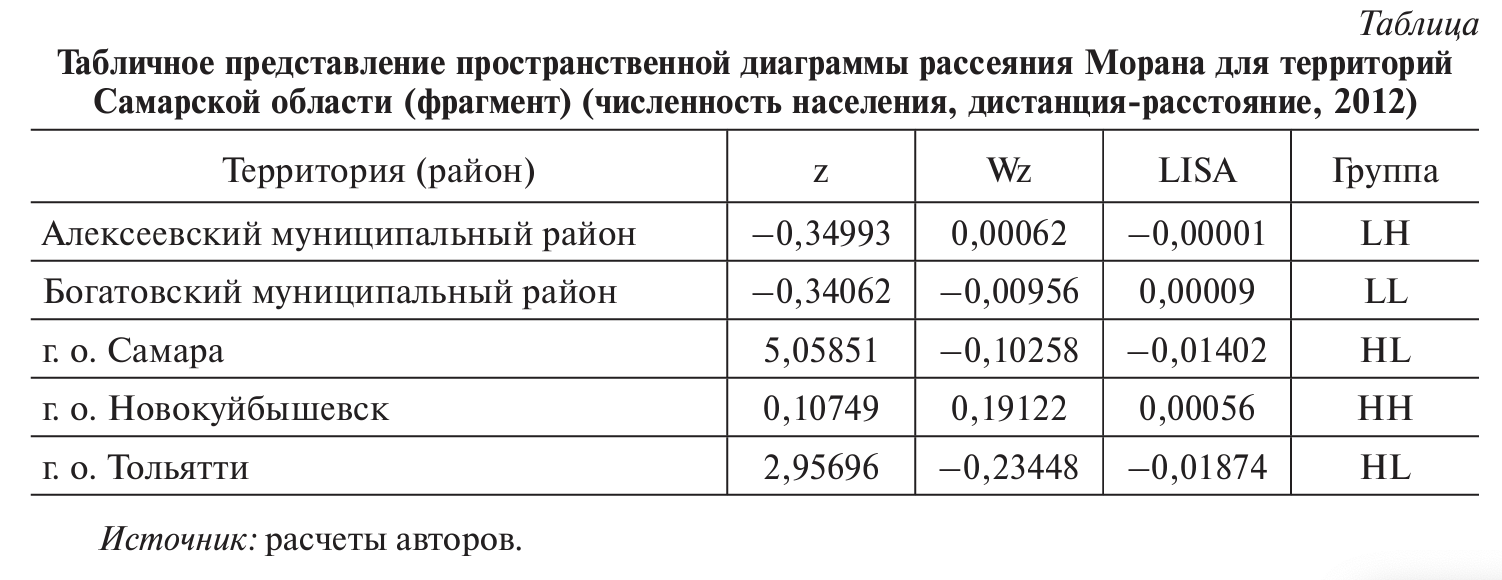
Как видно на диаграмме (рис. 3), в Самарской области выявлено четыре кластера территорий.
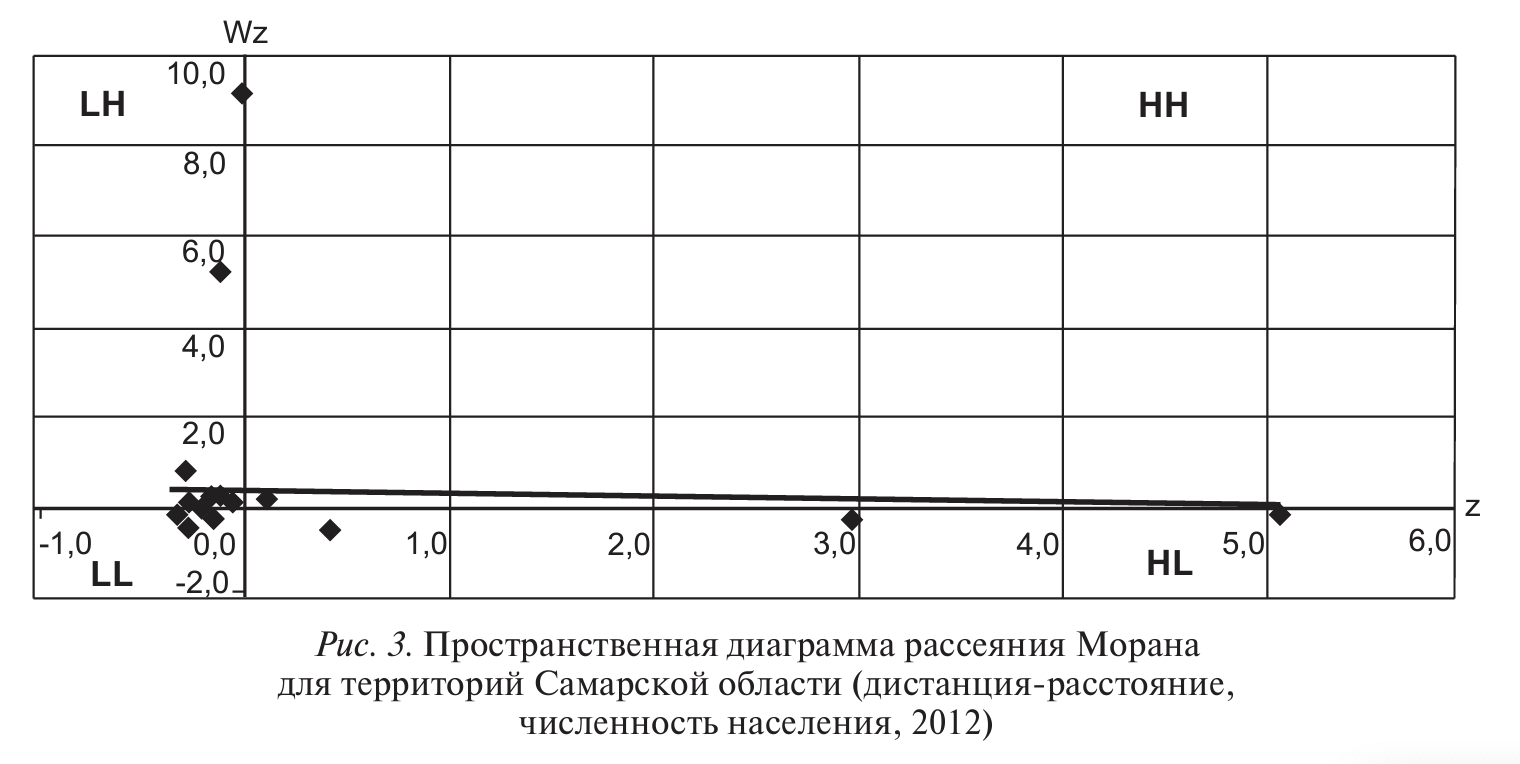
Выявленные кластеры можно представить на карте (рис. 4) и охарактеризовать как:
- ядра - г. о. Самара, Тольятти и Сызрань. Это территории, лежащие в квадранте HL на диаграмме пространственного рассеяния Морана. Территории в нем имеют относительно высокие собственные значения анализируемого показателя, окружены территориями с относительно низкими значениями анализируемого показателя. Автокорреляция отрицательная. Это своеобразные «экстремумы» повышенной концентрации населения на карте области, формирующие «опорный каркас»;
- спутник-противовес г. о. Самара - г. о. Новокуйбышевск. Это территории, лежащие в квадранте НН на диаграмме пространственного рассеяния Морана. Территории в нем имеют относительно высокие собственные значения анализируемого показателя, окружены территориями также с относи- тельно высокими значениями анализируемого показателя. Автокорреляция положительная. Расположенные в этом квадранте территории характеризуются тем, что похожи на территории с высокими показателями, но при этом не являются «экстремальными» для округи. То есть они не могут быть ядрами (нет превосходства над окружающими территориями), но не могут быть и периферией, т. к. собственные значения слишком высоки. На основании этого их можно отнести к спутникам-противовесам, чье взаимовлияние в основном сконцентрировано на ядрах;
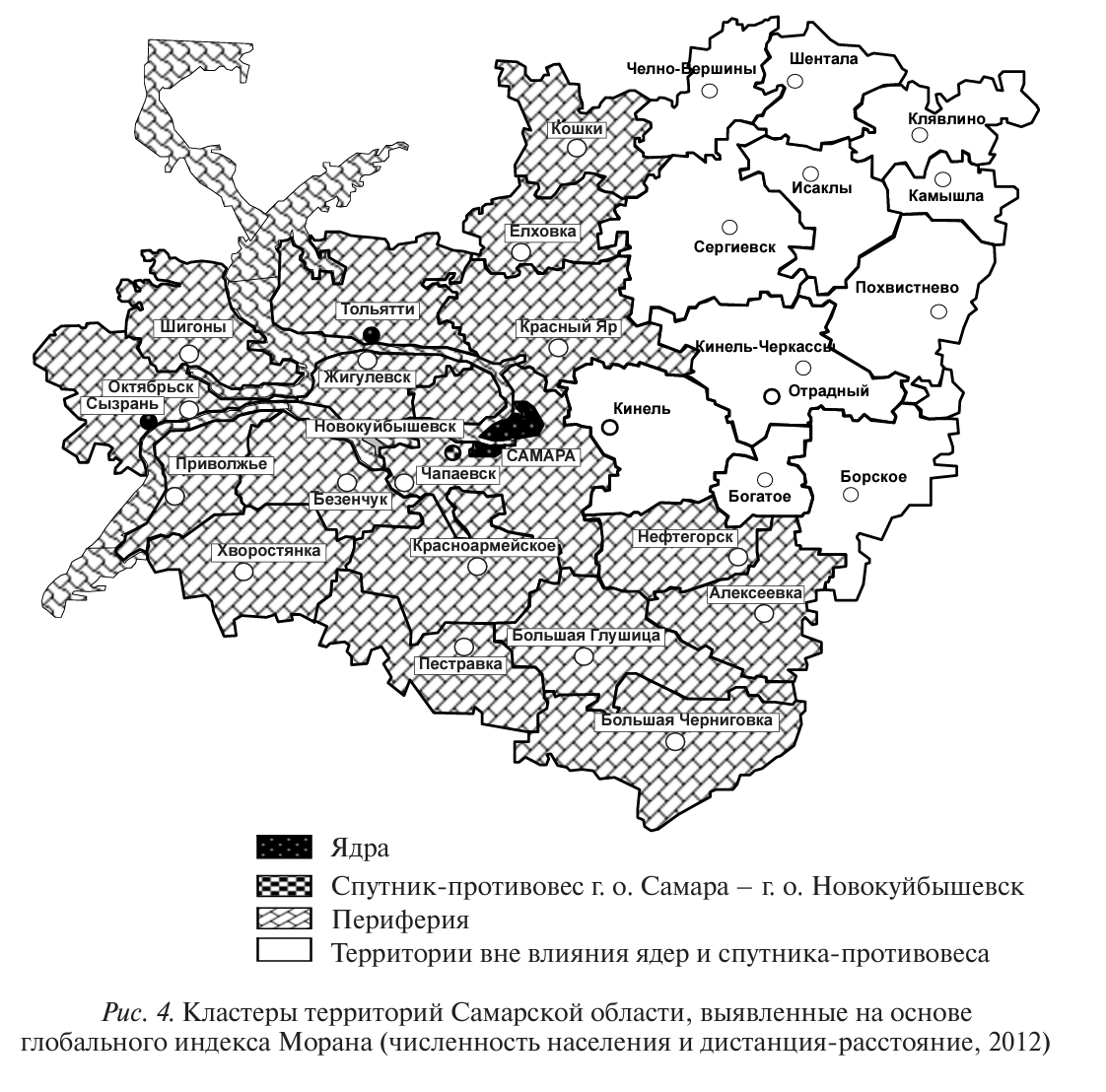
- периферия - территории, испытывающие повышенное влияние ядер и спутника-противовеса г. о. Новокуйбышевск - 19 территорий (3 городских округа и 16 муниципальных районов). Это территории, лежащие в квадранте LH на диаграмме пространственного рассеяния Морана. Территории в нем
имеют относительно низкие собственные значения анализируемого показателя, окружены территориями с относительно высокими значениями анализируемого показателя. Автокорреляция отрицательная, т. е. к данному типу относятся территории, на которые простирается влияние территорий с высокими собственными значениями анализируемого показателя, это их своеобразная зона влияния. В рассматриваемом случае данный тип территорий испытывает влияние ядер и спутника-противовеса г. о. Самара. Соответственно, становится логичным отнесение данных территорий к периферии; - территории, не испытывающие влияния ни ядер, ни спутника-противовеса СТА - 14 территорий (3 городских округа и 11 муниципальных районов). Это территории, лежащие в квадранте LL на диаграмме пространстве иного рассеяния Морана; имеют относительно низкие собственные значения анализируемого показателя, окружены территориями также с относительно низкими значениями анализируемого показателя. Автокорреляция положительная.
Достоинством использования глобального индекса Морана явилось то, что он позволил объективно выявить три ядра. Недостатком является чрезмерная общность полученных результатов, т. к. степень влияния ядер на различные территории, относимые к периферии, неодинакова.
Локальный индекс Морана
Локальный индекс Морана (LISA) дает понимание силы автокорреляции между соседними территориями. Чем больше значение LISA по модулю, тем сильнее подобие/различие территории с территориями-соседями.
Построение пространственной диаграммы рассеяния Морана позволило выявить 4 кластера территорий. В рамках каждого кластера можно выявить подкластеры, образованные территориями со схожими значениями степени автокорреляции (выраженное по модулю LISA). Например, территории периферии в разной степени испытывают на себе влияние ядер. В качестве критерия отнесения территории к тому или иному подкластеру мы использовали значения LISA по модулю (рис. 5):
- ядра - г. о. Самара, Тольятти, Сызрань. Это группа территорий квадранта HL;
- спутник-противовес г. о. Самара - г. о. Новокуйбышевск. Это территории, лежащие в квадранте НН;
- зона сильного влияния ядер и спутника-противовеса г. о. Самара - 3 муниципальных района. Это группа территорий с наибольшими по модулю значениями LISA (от [0,00377] и больше), входящих в квадрант LH. Чем выше значения по модулю LISA, тем сильнее взаимосвязь территории с окружением. Так как была проведена кластеризация в квадранте LH, т. е. среди территорий под влиянием ядер, то были выявлены территории с наиболее заметным влиянием ядер;
Ядра
Спутник-противовес г. о. Самара - г. о. Новокуйбышевск
I I Зона сильного влияния ядер и Новокуйбышевска
Зона слабого влияния ядер и Новокуйбышевска
II I I I Противовес ядрам
I I Территории вне влияния ядер и спутника-противовеса
Рис. 5. Подкластеры территорий Самарской области, выявленные
на основе локального индекса Морана (LISA) (численность населения
и дистанция-расстояние, 2012)
- зона слабого влияния ядер и спутника-противовеса г. о. Самара - 16 территорий (3 городских округа и 13 муниципальных районов). Это группа территорий с меньшими по модулю значениями LISA (до [0,00377]), входящих в квадрант LH;
- противовес ядрам - г. о. Похвистнево и Похвистневский район, г. о. Кинель. Это группа территорий, у которых значения LISA по модулю сравнимы со значениями ядер (от [0,00109] до [0,00369]), входящих в квадрант LL. Но при этом они не испытывают влияние ядер (т. к. находятся в квадранте LL). Численность населения в этих территориях значительна, взаимовлияние с окружающими территориями также значительно, соответственно, их можно отнести к новым «точкам роста»;
- зона вне влияния ядер и спутника-противовеса - 11 территорий (1 городской округ и 10 муниципальных районов). Это группа территорий с меньшими по модулю значениями LISA (до [0,00109]), входящих в квадрант LL
Полученные результаты дают более детальное представление о пространственных взаимодействиях по сравнению с глобальным индексом Морана. Территории теперь разделены по степени влияния ядер и спутника-противовеса, кроме того, выявлена зона противовеса ядрам - г. о. Похвистнево и По- хвистневский район, г. о. Кинель.
Недостатком использования локального индекса Морана является то, что невозможно рассмотреть зону влияния конкретного ядра, т. к. происходит выявление кластеров для всего массива территорий Самарской области. Например, г. о. Новокуйбышевск, по логике, должен все же относиться к зоне влияния Самары, но оценки, основанные на локальном индексе Морана, этого не учитывают.
Следовательно, возникает потребность в выявлении:
- зоны влияния для каждого конкретного ядра;
- зоны совместного влияния нескольких ядер.
Решить данную задачу предлагается на основе использования составляющих локального индекса Морана.
Составляющие локального индекса Морана
Рассмотрим зоны влияния Самарского ядра. Выявление зон влияния Самарского ядра осуществлено на основе числовых значений по модулю, полученных из составляющих локального индекса Морана и характеризующих степень взаимовлияния Самары и каждой конкретной территории с учетом автокорреляции. В результате получена новая конфигурация границ Самарского ядра (рис. 6):
- зона сильного влияния Самарского ядра - г. о. Самара, Тольятти, муниципальные районы Волжский, Кинельский, Красноармейский. Это группа территорий, которые обладают наибольшими значениями LISA по модулю (от [0,00134] и выше). Соответственно, это зона с наиболее сильным взаимовлиянием с Самарой;
- зона среднего влияния Самарского ядра - г. о. Сызрань, Новокуйбышевск, Кинель, а также 9 муниципальных районов. Это группа территорий со средними значениями LISA по модулю, переходными между высокими и стремящимися к нулю значениями (от [0,00060] до [0,00134]);
- зона слабого влияния Самарского ядра - г. о. Чапаевск, Октябрьск, Отрадный, Похвистнево, 15 муниципальных районов. Территории данной зоны характеризуются значениями LISA по модулю, стремящимися к нулю (до [0,00060]). Соответственно, взаимовлияние с Самарой слабое или почти отсутствует.
Рис. 6. Зоны влияния Самарского ядра, выявленные на основе составляющих локального индекса Морана (LISA) для г. о. Самара (численность населения и дистанция-рас стояние, 2012)
Надо полагать, что наличие зоны слабого влияния Самары связано с наличием сильных (по LISA) территорий, оказывающих влияние на зону слабого влияния Самары и тем самым «нивелирующих» влияние Самары. Это могут быть такие городские округа, как Тольятти, Сызрань, Похвистнево и др. Таким образом, можно уточнить границы Самарского ядра, существенно расширив их.
Аналогичный анализ можно выполнить для других ядер - Тольятти, Сызрани, как, впрочем, и для любой другой территории региона.
Далее, на следующем этапе исследования, можно выявить интересующие ядра и зону их максимального влияния. Кроме того, можно выявить зону влияния совокупности ядер, рассматривая их уже как единый объект. При этом возможен случай, когда территория (район), ранее не относившаяся к зоне влияния ни одного из ядер, теперь может оказаться в зоне агломерации из-за совместного, синергетического влияния сразу нескольких ядер.
В качестве примера представим на карте зоны совместного влияния Самары и Тольятти (рис. 7). Выявление зон совместного влияния двух ядер производилось на основе числовых значений по модулю, полученных из составляющих локального индекса Морана и характеризующих степень взаимовлияния системы Самара - Тольятти и каждой конкретной территории с учетом автокорреляции.
Как видно, сформирована новая конфигурация границ при предположении о существовании только двух ядер:
1) зона сильного влияния системы Самара - Тольятти - г. о. Самара, Тольятти, муниципальные районы Волжский, Ставропольский. Это территории, которые обладают наибольшими значениями LISA по модулю (от [0,00383] и выше). Соответственно, это зона с наиболее сильным взаимовлиянием с системой Самара - Тольятти. Данную зону логично отнести к ядру;
I I Зона слабого влияния системы Самара - Тольятти
Рис. 7. Зоны влияния объединенной системы Самара - Тольятти, выявленные на основе составляющих локального индекса Морана (LISA) (численность населения и дистанция-расстояние, 2012)
- зона среднего влияния системы Самара - Тольятти - г. о. Сызрань, Октябрьск, Новокуйбышевск, Жигуле век, Кинель, 8 муниципальных районов. Это территории со средними значениями LISA по модулю, переходными между высокими и стремящимися к нулю значениями (от [0,00091] до [0,00383]). Данную зону логично отнести к периферии, где влияние ядер заметно;
- зона слабого влияния системы Самара - Тольятти - г. о. Панаеве к, Отрадный, Похвистнево, 17 муниципальных районов. Территории данной зоны характеризуются значениями LISA по модулю, стремящимися к нулю (до [0,00091]). Соответственно, взаимовлияние с системой Самара - Тольятти слабое или почти отсутствует.
Таким образом проведенное исследование наглядно показывает возможности использования глобального и локального индексов Морана для выявления кластеров и подкластеров, определяемых силой пространственных взаимодействий. Использование при определении индексов Морана различных параметров позволяет выявить варианты территориальных кластеров и подкластеров. Это дает возможность оценить пространственные эффекты принимаемых управленческих решений и найти их оптимум в зависимости от поставленных целей.
При этом необходимо отметить, что расчет характеристик пространственной корреляции является лишь предварительным этапом пространственного эконометрического анализа. Указанные характеристики свидетельствуют о наличии, но не объясняют причин образования территориальных кластеров. Выявление этих причин является предметом дальнейших исследований.
СПИСОК ЛИТЕРАТУРЫ
- Автомобильный портал грузоперевозок. URL: www.avtodispetcher.ru (дата обращения: 14.05.2014).
- Автомобильный портал грузоперевозок. URL: www.samara-oblast.ru (дата обращения: 10.03.2014).
- Балаш О.С. Пространственный анализ размещения торговых предприятий Саратова // Поволжский торгово-экономический журнал. 2010. № 4. С. 13–22.
- Беляева А.В. Использование пространственных моделей в массовой оценке стоимости объектов недвижимости // Компьютерные исследования и моделирование. 2012. Т. 4. № 3. С. 639–650.
- Вакуленко Е.С. Введение в пространственную эконометрику / М.: НИУ ВШЭ, 2013. URL: http://pokrovka11.files.wordpress.com/2013/01/spatial_econometrics.pdf (да-та обращения: 03.01.2014).
- Демидова О.А. Выявление пространственных эффектов для основных макро-экономических показателей российских регионов. НИУ ВШЭ. 2013. URL: http://www.hse.ru/data/2013/12/03/1335971579/Demidova_Article_HSE_2013.pdf (дата обращения: 25.06.2014).
- Дубровина Н.А. Применение методов пространственной эконометрики в региональных исследованиях. Бизнесинформ. 2010. № 5 (2).
- Зверев Д.В., Коломак Е.А. Субфедеральная фискальная политика в России: межрегиональные различия и связи. Серия «Научные доклады: независимый экономический анализ» / Московский общественный научный фонд; Сибирский центр прикладных экономических исследований. М., 2010. № 209. 102 с.
- Федеральная служба государственной статистики. URL: http://www.gks.ru (дата обращения: 05.07.2014)
- Экономико-географические и институциональные аспекты экономического роста в регионах / Консорциум по вопр. приклад. экон. исслед., Канадское агентство по международ. развитию; О. Луговой и др. М.: ИЭПП, 2007. 164 с. URL: http://www.iep.ru/files/text/cepra/Rost_v_reg_rus.pdf (дата обращения: 05.05.2014).
- Электронный учебник по статистике / StatSoft, Inc., 2012. URL: http://www.statsoft.ru/home/textbook/default.htm (дата обращения: 04.01.2014).
- Anselin L. Local Indicators of Spatial Association — LISA // Geographical Analysis. 1995. Vol. 27 (2). С. 93–115. DOI: 10.1111/j.1538-4632.1995.tb00338.x
- Chen Y. New Approaches for Calculating Moran’s Index of Spatial Autocorrela-tionm. 2013. PLoS ONE 8(7): e68336. DOI: 10.1371/journal.pone.0068336
- Coro Chasco Yrigoyen. Course on Spatial Econometrics with Applications. Session 2: Spatial Effects. 2007. URL: http://www.uam.es/personal_pdi/economicas/coro/docencia/doctorado/spateconUPC/Slides/Session2_Spatial effects_Notes.pdf (дата обращения: 05.01.2014).
- Danlin Yu. Spatial Association and Spatial Statistic Techniques. 2003. URL: http://www.uwm.edu/People/danlinyu/Spatial_Association.ppt (дата обращения: 03.01.2014).
- Introduction to Spatial Analysis. Invited Lecture. Population Science and GIS Workshop, UC Santa. 2006.
- Local Measures of Spatial Autocorrelation / Briggs Henan University. 2010. URL: http://www.utdallas.edu/~rbriggs/henan/11SAlocal.ppt (дата обращения: 06.01.2014).





