Effect size, confidence intervals and statistical power in psychological research


Published: Sept. 10, 2015
Latest article update: Dec. 23, 2022
Abstract
Quantitative psychological research is focused on detecting the occurrence of certain population phenomena by analyzing data from a sample, and statistics is a particularly helpful mathematical tool that is used by researchers to evaluate hypotheses and make decisions to accept or reject such hypotheses. In this paper, the various statistical tools in psychological research are reviewed. The limitations of null hypothesis significance testing (NHST) and the advantages of using effect size and its respective confidence intervals are explained, as the latter two measurements can provide important information about the results of a study. These measurements also can facilitate data interpretation and easily detect trivial effects, enabling researchers to make decisions in a more clinically relevant fashion. Moreover, it is recommended to establish an appropriate sample size by calculating the optimum statistical power at the moment that the research is designed. Psychological journal editors are encouraged to follow APA recommendations strictly and ask authors of original research studies to report the effect size, its confidence intervals, statistical power and, when required, any measure of clinical significance. Additionally, we must account for the teaching of statistics at the graduate level. At that level, students do not receive sufficient information concerning the importance of using different types of effect sizes and their confidence intervals according to the different types of research designs; instead, most of the information is focused on the various tools of NHST.
Keywords
Confidence intervals, effect size, NHST, statistical power
Introduction
In the last three decades, a critical movement occurring within quantitative psychological research began to develop. This development emerged in response to the misguided use of classical statistics based on null hypothesis significance testing (NHST). NHST promotes dichotomous thinking and provides limited information regarding the essence of investigated phenomena. Dichotomous thinking in science — manifested as only accepting or rejecting research hypotheses — prevents the advancement of science and may even skew the accumulation of knowledge by stimulating the exclusive publication of studies whose hypotheses have been accepted. The so-called “new statistics” movement critically challenges NHST postulates and operations. This movement is an approach based on the analytical tool of estimation (Cummings, 2014), which promotes the use of effect size as descriptive statistic, confidence intervals as inferential statistics, and meta-analysis as a reliable form of knowledge accumulation. This paper is intended to analyze the disadvantages of NHST and the advantages of using effect size, confidence intervals and statistical power in quantitative psychological research, especially in clinical studies. Also noted and stressed is the need for editors of scientific psychological journals to adhere to policies recommended by the A.P.A. in this regard.
Quantitative research in psychology
Typically, quantitative psychological research is focused on detecting the occurrence of certain population phenomena by analyzing data from a sample. An example is the case in which a researcher wishes to know if a treatment to improve the quality of life of those who suffer from breast cancer performs better than a placebo treatment for another group or those on a waiting list (also known as the control group or contrast group) (Wilkinson, 1999). Similarly, to make the decision to confirm that an independent variable or treatment did or did not have an important effect, statistics is used. In quantitative research methodology, there are two ways of quantifying this effect: (1) Null Hypothesis Significance Testing and (2) Effect Size (ES), as well as its respective confidence intervals (Cl). These two approaches are reviewed below.
Null Hypothesis Significance Testing (NHST)
NHST comes from the effect size on the population, the size of the sample used and the alpha level or p value that is selected (p being the abbreviation for probability). Most psychology research is focused on rejecting the null hypothesis and obtaining a small p value instead of observing the relevance of the results that are obtained (Kirk, 2001).
Among the limitations of NHST, we found its sensitivity to sample size, its inability to accept the null hypothesis, and its lack of capacity to determine the practical significance of the statistical results.
Kirk (2001) states that NHST only establishes the probability of obtaining a more or less extreme effect if the null hypothesis is true. It does not, however, communicate the magnitude of the effect or its practical significance, meaning whether the effect is found to be useful or important. As a result, inferential statistical testing has been criticized; as expressed by Ivarsson, Andersen, Johnson, and Lindwall (2013): “p levels may have little, if anything, to do with real-world meaning and practical value” (p.97). Some authors, such as Schmidt (1996), even suggest that statistical contrast is unnecessary and recommend focusing only on ES estimation, and Cohen (1994) suggests that “NHST has not only failed to support the advance of psychology as a science but also has seriously impeded it.” (p. 997).
Ronald Fisher was the father of modern statistics and experimental design. Since his time, it has been established as a convention that the p value for statistical significance must be less than .05, which means that an observed difference between two groups has less than a 5% probability of occurring by chance or sampling error if the null hypothesis is assumed to be true initially. In other words, if the p was equal or less than .05, then the null hypothesis could be rejected because 95 times out of 100, the observed difference between the means is not due to chance. Some researchers use more strict significance levels, such as p<.01 (1%) and p < .005 (0.5%). The convention of p < .05 has been used almost blindly until now. The question is why a different p value has not been agreed upon, for example, .06 or .04. Indeed, there is no reason or theoretical or practical argument that sustains the criterion ofp > .05 as an important cut-off point. This circumstance has led some statistical experts and methodologists, such as Rosnow and Rosenthal (1989), to express sarcastically that “Surely, God loves the .06 nearly as much as the .05.” (p. 1277).
NHST is deeply implanted in the mind of researchers who encourage dichotomous thinking, a type of thinking that perceives the world only black or white world, without intermediate shades (Kirk, 2001). From the perspective of NHST, results are significant or not significant, and even worse, this approach has led to the idea that if the results are significant, they are real, and if they are not significant, then they are not real, which has slowed the advancement of science. Furthermore, this approach has provoked researchers not to report the data from their work because they consider such data to be not significant; their reasoning is that “there were no important results” or that the “hypothesis was not proved.” Moreover, publishing only the statistically significant data in scientific journals skews the corresponding knowledge and gives the wrong idea about psychological phenomena (Cum- ming, 2014). For that reason, Cumming (2014) has proposed that we consider the so-called “new statistics,” the transition from dichotomous thinking to estimation thinking, by using ES, confidence intervals and meta-analysis.
Some authors (Cumming, 2014; Schmidt and Hunter, 2004; Tressoldi, Giofre, Sella, & Cumming, 2013) summarize the difficulties of NHST as follows:
- NHST is centered on null hypothesis rejection at a level that was previously chosen, usually .05; thus, researchers shall obtain only an answer to “if there is or is not a change that is different from zero”.
- It is probable that the p value is different if the experiment is repeated, which means that p values offer a very loose measure of result replicability.
- NHST does not offer an ES estimation.
- NHST does not provide information about accuracy and error probability from an estimated parameter.
- Randomness (in sampling or in participants’ assignments to groups) is one of the key pieces of the NHST procedure because without it such statistical contrasts are irrelevant when the null hypothesis is assumed to be false a priori. Nevertheless, there is no evidence that the null hypothesis is true with respect to attempting to reject it.
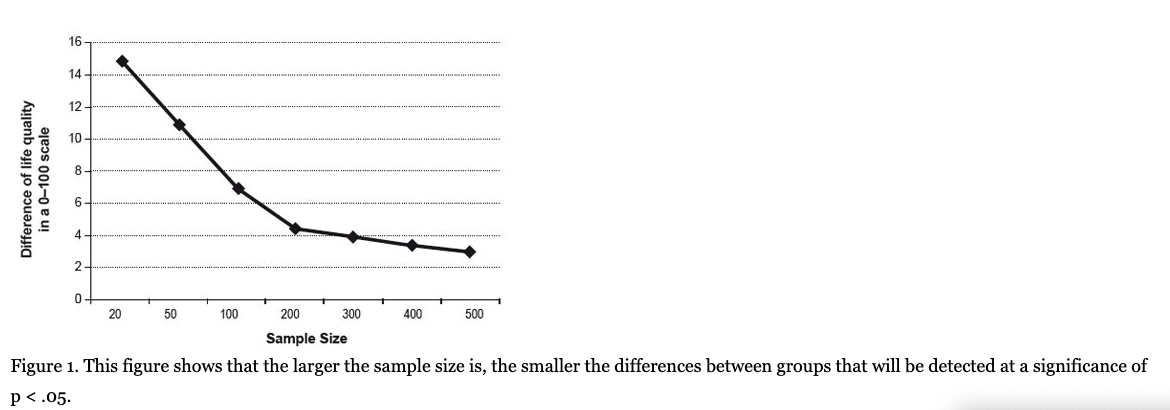
- The likelihood of rejecting the null hypothesis increases as the sample size increases; therefore, NHST tells us more about N than about the hypothesis. The interpretation of statistical significance becomes meaningless when the sample size is so large that any detected difference, however small or even trivial, shall allow the rejection of the null hypothesis. In this way, for example, when applying an intervention to a group of N = 50 compared with a control group of the same size, in a quality-of-life scale from 0 to 100 points, a difference of 10 points between the two groups will be needed to reach p < .05, but with a sample of 500 persons in each group, statistical significance can be reached with a difference of only 3 points (see Figure 1). The question is: for a treatment that produces a quality-of-life improvement of only 3%, is it important to patients regardless of whether it is statistically significant?
- Many researchers espouse the idea that the significance level is equal to causality, but it is not; statistical significance is only one element among many that enables us to discuss causality (Nyirongo, Mukaka & Kalilani- Phiri, 2008).
Some statisticians and researchers believe that not only is the NHST unnecessary, it has also damaged scientific development. As stated by Schmidt and Hunter (2002, p. 65): “Significance tests are a disastrous method for testing hypotheses, but a better method does exist: the use of point estimates (ESs) and confidence intervals (CIs).”
Why are NHSTs still used?
If NHST offers little information to prove a hypothesis, then the question becomes, why is it still used? Perhaps the explanation of their intensive use in psychological research can be found in the fact that most of the measurements are ordinal.
Inferential statistical tests have been used and are still used in making the decision to reject or accept a hypothesis. It is likely that the main attraction of NHSTs is their objectivity when establishing a criterion such as the p < .05 minimum value, which excludes researcher subjectivity; on the other hand, practical and clinical significance requires a subjectivity component. Often, researchers did not want to be committed to a decision that is impregnated into implicit subjectivity, for example, in terms of social relevance, clinical importance, and financial benefit. Nonetheless, in the foregoing, Kirk (2001) argues that science would gain greater benefits if a researcher was focused on the magnitude of an effect and its practical significance, believing as well that “No one is in a better position than the researcher who collected and analyzed the data to decide whether the effects are trivial or not” (p. 214).
Change of APA editorial policy (under pressure) regarding ES
For many years, critics of NHST, usually experts in statistics and methodology in social sciences and behavior, have recommend reporting-ES in addition to statistical significance (Wilkinson, 1999).
This pressure was especially high in the American Psychological Association (APA) and was reflected for the first time in the Publication Manual of the APA 4th ed. (1994), in which authors of research studies are “encouraged” to report the ES (p. 18). This soft recommendation, however, contrasted with rigid demands for less essential aspects, such as the order and form of the literature references.
In 1999, after a long period of work, Wilkinson and the APA Task Force on Statistical Inferences prepared a report that stated: “researchers must always publish the effect size in the main results” (p.599).
In response to Wilkinson and the Task Force recommendations, APA, in its Publication Manual, 5th ed. (2001), recommended the following to researchers: “For the reader to fully understand the importance of your findings, it is almost always necessary to include some index of the effect size or strength of the relationship in your Results section” (p.25). As observed, APA had yet to dare to fully endorse the use of ES.
In the sixth edition, APA (2010) stated that “NHST is but a starting point and that additional reporting elements such as effect sizes, confidence intervals, and extensive description are needed to convey the most complete meaning of the results” (p. 33). Additionally, it stated that a complete report of all of the hypotheses proven, effect size estimates and their confidence intervals are the minimum expectations for all APA journals (APA, 2010, p.33). In this last edition, APA already widely recommended the use of ES in addition to ES confidence intervals, and the fact that it affirmed that NHST “is but a starting point” indicates a very clear change in the method of analyzing and construing research results in psychology. This was a consequence of the pressure from outstanding researchers and statisticians, such as Cohen (1992a), Thompson (2002), Rosnow (1989), Rosenthal (1994), Schmidt and Hunter (2002), and Cumming (2014), among others.
Encouraging researchers to report ES and confidence intervals in their research studies greatly depends on the policies of scientific journals, as stated by Kirk (2001): “Journal editors are the gatekeepers for what appears in our scientific journals. They must be knowledgeable about good statistical practices and make authors adhere to those practices” (p. 217). It is expected that such a policy will be extended to all scientific journals in psychology. We consider, however, that journal editors’ attitudes are not the only obstacle and that graduate-level statistical training is also implicated (Aiken, West, Sechrest & Reno, 1990). There, students do not receive information and structured teaching regarding the use and importance of different types of ES and confidence intervals in different types of research designs, as the APA recommends; most of the information is focused on different types of NHST (e.g., t test, ANOVA, A2, among others).
Is ES being reported in scientific articles as recommended by the APA?
The foregoing has caused journal editors to increasingly request not only inferential statistics but ES, as well (Schmidt & Hunter, 2004). In 2004, there were already 23 important education psychology journals with editorial policies that indicated the need to report ES in research studies. Although many journals disregard APA recommendations, however, the number of research studies that report ES is increasing. For example, Mathews et al. (2008) analyzed 101 articles from 5 psychology journals for the period from 1996 to 2005 and found that the number of articles that reported ES in their results increased 26% from 1996 to 2000 and 46% from 2001 to 2005. On the other hand, McMillan and Foley (2011) analyzed 417 articles in 4 specialized journals in education and psychology that were published in the period from 2008 to 2010 and found that 74% of the studies reported ES measures. The most often used ES tests were Cohens d and eta2, with Hedges#, odds ratio, Cohens f, and omega2 being used less. When Cohens d was reported, it was generally followed by indications from the cited researcher (Cohen, 1992a), to interpret the results (0.2 = “small effect”, 0.5 = “medium effect” and 0.8 or higher = “large effect”). The percentage of articles that used this convention was very high (94%). Interestingly, these authors noted that half of the sample articles’ authors did not construe the ES results; they only reported Cohen’s value, which shows a lack of knowledge of the ES relevance in the research that was performed (McMillan & Foley, 2011).
Not all editors of high-impact scientific journals request their authors to use the best statistical standards; for example, journals that are very prestigious, such as Nature and Science, only report statistical significance test reports of a null hypothesis in 89% and 42% of their articles, respectively, without reporting the SE or confidence intervals, among other statistical tests that measure the magnitude of an effect. In contrast, other magazines with less impact, such as Neuropsychology, Journal of Experimental Psychology-Applied and American Journal of Public Health, do report SE or their confidence intervals; the foregoing has excited the question from some authors as to whether high impact is equal to high statistical standards in scientific journals, and the answer is no (Tressoldi et al, 2013).
It is noteworthy that the Basic and Applied Social Psychology (BASP), a prestigious journal in the field of social psychology, recently communicated to researchers interested in publishing in it the decision to ban NHST procedures from BASP. The editorial note states that:
“If manuscripts pass the preliminary inspection, they will be sent out for review. However, prior to publication, authors will have to remove all vestiges of the NHST procedures (p-values, t-values, F-values, statements about significant’ differences or lack thereof, and so on)” (Trafimow & Marks, 2015, p.l).
But, incredibly, at least for us, they also banned the use of confidence intervals because CIs and p-values are based on the same statistical theory. BASP does encourage the use of descriptive statistics, such as effect sizes (Trafimow & Marks, 2015).
Concerning educational research, the American Educational Research Association (AERA, 2006) recommends that research statistical results include a size effect of any type as well as the respective confidence intervals, and the in case of a hypothesis evaluation, the respective statistical tests.
The winds of change have also arrived in the field of medicine. The 2014 document “Recommendations for the Conduct, Reporting, Editing, and Publication of Scholarly work in Medical Journals” from the International Committee of Medical Journal Editors (ICMJE) contains the following recommendation: “Avoid relying solely on statistical hypothesis testing, such as p values, which fail to convey important information about effect size and precision of estimates” (p. 14). More and more frequently, opinions with respect to NHST have little to offer, and they must not be used in medical research. For example, the Chief-in-Writing of the Revista Panamericana de Salud Publica, criticizing the use of NHST in research, stated that “Researchers who obtain (statistically) significant results have previously been satisfied when reaching their goal, without realizing that they have not achieved an improvement, in any way, to the understanding of the phenomenon being studied” (Clark, 2004, p.293). Next, we will describe the effect size in detail.
Effect size
It is clear that NHSTs alone are insufficient to evaluate the effect of a treatment; they must be supplemented by further information to determine more precisely the impact of an intervention or the strength of the relationship between two or more variables. One of these tools is the statistical unit that is known as the effect size.
ES is defined as the magnitude of impact of an independent variable over a dependent variable; it can be expressed in a general way as the size or strength of the relationship between two or more variables (Rosenthal, 1994). An ES also represents a standardized value that calculates the magnitude of the differences between groups (Thomas, Salazar & Landers, 1991). Synder and Lawson (1993) state that ES directly indicates the degree to which a dependent variable can be controlled, predicted, or explained by an independent variable. In this way, ES refers to the magnitude of an effect that is, in this example, the difference between group A (which received the treatment) and group В (which did not). If the treatment effects in group A are truly notable compared with those of the control group, then we want to know the magnitude or size of this effect, and consequently, the extent to which this phenomenon is expected to occur over the entire population.
An ES is a direct way of measuring the effectiveness of a specific intervention because it is independent of the sample size and the measurement scale; moreover, considering the changes in both the scores and the variation (standard deviation) would allow us to know understand how relevant the interventions are.
In summary, we can state that ES is useful to: 1) estimate the sample size that is required to obtain an acceptable statistical power (0.80); 2) integrate the results from a series of empirical research studies in a meta-analysis study; 3) complement NHST data, and 4) determine whether research results are significant from a practical standpoint (Kirk, 2007). SEs can be useful in the following cases:
1 - To identify the magnitude of a treatment effect in a determined group (pre-test and post-test).
2 - To see the efficacy of a treatment compared with other groups (control group and intervention group).
3 - To identify changes through time in a determined group; all of the data must be on a common standardized scale.
4 - To identify the degree of correlation between two or more variables.
Types of ES
Broadly, ES is a term that is used to describe a family of indices that measures the effect size of a treatment (Rosenthal, 1994), and Cohen’s d is one of those indices. To observe the difference between a control group (Xcon) and an experimental group (Xexp), the means of both groups are compared, and that difference is divided by the pooled standard deviation of both groups. The pooled standard deviation is found as the root mean square of the two standard deviations. This index was proposed by Cohen (1992b), who identified it using the letter d. He was the first to highlight the importance of the effect size in psychological research.
Researchers have long discussed whether the standard deviation used to obtain ES must be the one proposed by Cohen (1988), the combined standard deviation or the pooled standard deviation of both groups, which is as follows:
On the other hand, Gene Glass (Smith & Glass, 1977) proposed using only the SD of the control group (SD con), which is identified by the Greek symbol Д and is called “Glass’s delta” because according to this researcher, this SD is not affected by the independent variable and is consequently a more genuine representation of the population’s SD.
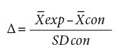
Instead, Cohen (1988) proposes using the pooled SD of both groups, arguing that the two groups contribute to the differences, and when linking the N of the two groups, an SD that is more similar to the population SD can be obtained instead of a sole group’s SD.
Some authors (Huberty, 2002) believe that the NHST and ES metrics offer mutually complementary information: ES indicates the magnitude of the effect that is observed or the strength of the relationship between the variables, while the p-value indicates only the probability that this effect or strength of the relationship is due to chance, although the latter is better shown by confidence intervals (Cumming, 2014).
Conversely, the ES values (d) can be expressed in standardized units using a ranking that ranges from -3.0 to +3.0. Cohen (1992a, 1992b) argues that the comparison between the two groups shows that the degree of ES magnitude must be divided into three types (see Table 1).
Table 1. Interpretation of the results on d according to Cohen’s (1992) recommendations
Cohen's d effect size | Interpretation | Differences in SD |
d=.0-.19 | Trivial effect | <1/5 from a SD |
d= .20 | Small effect | 1/5 from a SD |
d= .50 | Medium effect | 1/2 from a SD |
d=.80 or higher | Large effect | 8/10 from a SD |
Table 2. Formal techniques that allow ES quantification
Type of research | Indices of effect size | NHST | Effect size |
Differences between 2 groups | Cohen’s d | Student t | 0.20 small |
Differences between 3 or more groups. | Square Eta (η2) | ANOVA | 0.01 small |
Retrospective study or case control study | Odds ratio (OR)
|
| 1.5 small
|
Cramer’s Phi(φ) | Square Chi (x2) | 0.10 small | |
Bivariate correlation | Coefficient of product- moment correlation (r) |
| 0.10 small |
| Coefficient of determination (r2) |
| 0.01 small |
Diverse formal techniques that allow ES quantification have been developed for diverse statistical tests, including the t test, r correlational analysis, and analysis of variance, among others (See Table 2). These ES estimation techniques have a practical application in psychology, and they offer common metrics by which the research results of a meta-analysis can be integrated.
The ES calculation can be performed regardless of whether p was significant (Rosnow & Rosenthal, 1989) for the following reason: ES can guide the sample size that is necessary in future studies because in every statistical test, the power of the test (understood as the capacity to reject the null hypothesis as being false) is determined by the p level, sample size and effect size. These 3 aspects are so interrelated that when two of them are known, the third one can be easily determined. Knowing the p level and effect size, it is possible to determine the sample size that is required to obtain the desired significant statistical result. In this way, if the results from the research are not statistically significant but present practical significance, meaning that there is a medium or large ES, then to obtain statistical significance, it would only be necessary to increase the sample size. Similarly, the higher the ES, the smaller the sample size that is required to detect a significant p value (See Figure 2).
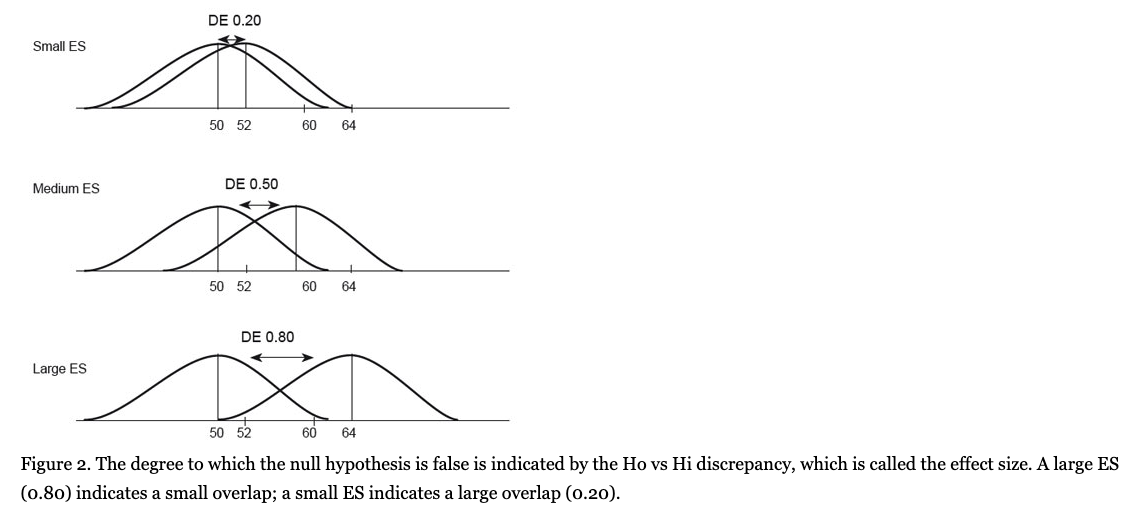
With regard to the ES values that are classified as small, medium and large, Cohen (1992b) expressed the following: “My intent was that medium ES represent an effect likely to be visible to the naked eye of a careful observer... I set small ES to be noticeably smaller than medium but not so small as to be trivial, and I set large ES to be the same distance above medium as small was below it.” (p. 99) (See Table 3).
Table 3. ES magnitude, its percentile rank and non-overlapping percentages
Effect magnitude according to Cohen | Cohen’s d effect size | Percentile rank | Non-overlapping percentage |
Small | 0.0 | 50.0 | 0% |
0.1 | 54.0 | 7.7% | |
0.2 | 58.0 | 14.7% | |
0.3 | 62.0 | 21.3% | |
Medium | 0.4 | 66.0 | 27.4% |
0.5 | 69.0 | 33.0% | |
0.6 | 73.0 | 38.2% | |
0.7 | 76.0 | 43.0% | |
Large | 0.8 | 79.0 | 47.4% |
0.9 | 82.0 | 51.6% | |
1.0 | 86.0 | 58.9% |
Correlation Coefficient: A Type of Effect Size
Correlation is defined as the degree to which two variables covariate, meaning that two variables are correlated if they jointly vary. Usually a correlation coefficient is used (e.g., Pearsons r) to measure the degree of strength and direction (negative or positive) of this association, the formula for which is the following:
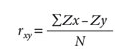
The correlation coefficient or “r” is perhaps one of the most common measures of ES. The correlation coefficient expresses the degree to which the subjects are similarly ordered in two variables, simultaneously. Similar to the d value, Cohen established r=.10 or more to be a small effect size; r=.30 or more to be a medium effect size; and r > .50 to be a large effect size (Hemphill, 2003).
It is possible to convert the value from any statistical test into a correlation coefficient; for example, the results of independent-sample t-tests can be converted to an effect size that is called equivalent r, and its formula appears below (Rosenthal & Rubin, 2003):
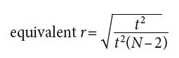
In addition, when the chi square (x2) value is known, the effect size can be obtained with the following formula:
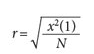
On the other hand, when the correlation coefficient r is squared, we obtain the coefficient of determination (r2), which indicates the proportional covariation of a variable with respect to another variable. If r2 is multiplied by 100, then a common variability percentage between the variables is obtained. Thus, r=.10, which Cohen considers to be small, shall have a coefficient of determination of 1%, and r=.20 or medium has a coefficient of determination of 4%, and a large r of .50 has 25% (Morales-Vallejo, 2008). When r=.50, it means, for example, that variable X explains 25% of the variability in Y.
The Mann-Whitney U test
The Mann-Whitney U test is a non-parametric alternative to the independent-samples t test in the case of non-normality. The effect size for the Mann-Whitney U is calculated as follows:
Where n1 + n2 is the total number of observations on which z is based. The calculation of the effect size of the Wilcoxon Signed-rank test as a non-parametric alternative to the paired-samples is given by the same formula.
On the other hand, sometimes it is highly useful to convert estimators such as Cohen’s d into r. This conversion facilitates the posterior carry out of meta-analyt- ical studies. The value of d can be converted into an rvalue by using the following formula (Ferguson, 2009):
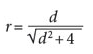
In turn, r can be converted into Cohens d using the following formula:
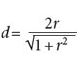
It is important to establish that r is an ES in itself and that the strength of this association can be small, medium or large, but when a p value is desired, one should consider the sample size of the study in addition to the ES, as the sample size would indicate the probability that the determined rvalue occurred by chance. In this way, an r= .50 (large ES) could be statistically significant if the sample size is n = 14 or higher, but in a sample of n = 13 or less, it would not be statistically significant, even if ES continued to be practically significant.
It is also important to note that although the correlation coefficient (r) and regression (R2) are types of ES, few researchers recognize them and report them as such (Alhija & Levy, 2009).
Other types of ES
When a study presents the means of the results from a control and experimental group with their respective standardized deviations, the interpretation is simple, but when the proportion of patients who improve, did not improve or became worse is presented in a clinical study, the interpretation is more difficult. In this case, the results of the association strength of the relationship are presented as a rank of possibilities or odds ratios (ORs), which is frequently used in clinical studies, especially in cases and controls or retrospective research. An OR is a measure of the association between an exposition and a result; in other words, it expresses the possibility that a result occurs in a determined condition compared with the possibility that the result occurs when it is not exposed to such a condition (Szumilas, 2010).
An important concept in ORs is “the event,” which refers to the proportion of patients who presented a specific result; this can be negative (disease or death) or positive (recovery from a disease) in both the intervention group and control group.
The foregoing is possible if the result is a dichotomous variable, a discrete event that can appear or not (sick/healthy). Although the odds ratio addresses only dichotomous data, showing the presence or absence of something, it can appear partially dichotomous with some degree of improvement or worsening. The latter type of data, however, must be transformed into dichotomous values by specifying a cut-off point on the degree of improvement that reflects an important change; consequently, the proportion of patients above or below such a cut-off point can be obtained.
For that purpose, a 2x2 table is used to present the results from a clinical study.
Table 4. In this 2x2 table, a treatment group and a control group and their improved self-esteem
| Improved self-esteem HSD | |
Yes | No | |
Intervention group | 9 | 9 |
Control group | 4 | 13 |
This example presents results from a study using hypnotherapy. These results show a group of women with breast cancer in which an observation was made on hypnotherapy’s effect on self-esteem compared with a control group. The results were that 50% of the intervention group of women obtained a positive change of Vi standard deviation, which is considered to be clinically significant, while at the same time, only 23% of the control group of women improved. The odds ratio value is 2.75, indicating that the effect size is between medium and large (because ES to OR= 1.5 is small, OR = 2 medium and OR = 3 is large in size according to Maher et al., 2006), with a 95% confidence interval [0.63 to 11.9], meaning that it is statistically significant. In other words, the exposure to hypnotherapy increases (by more than double) the self-esteem (2.75 times) of the women with breast cancer compared with the control group.
Additionally, the Phi coefficient (ф) is used to evaluate the magnitude of association in the chi-square (X2) 2x2 contingency tables. Phi is a Pearson product-moment coefficient that is calculated with two nominal and dichotomous variables in which the categories could be yes/no or 1/0. Phi is obtained very simply: it is the square root of the result of dividing X2 by N.
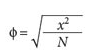
When the tables are larger than 2x2 (for example, 3 x 2 or 2 x 4) and we want to measure the strength of an association, we use Cramer V by considering the following formula:
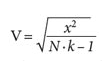
where к is the number of groups that are being compared.
Confidence intervals on the ES
Confidence intervals around the effect sizes offer improved accuracy of results because they disclose, in addition to the strength of the association between variables, their direction and the plausible range of an effect as well as the likelihood that the results are due to chance (as is accomplished by NHST) (Grimes & Schulz, 2002). The reason some authors suggest that research designs should be supported by such statistical tools as the effect size and confidence intervals (Cummings, 2014) is that the confidence interval is much more informative than the p value because “it indicates the extent of uncertainty, in addition to providing the best point estimate of what we want to know” (p. 13). Moreover, the advantage of confidence intervals is that they facilitate data interpretation and easily detect trivial effects, allowing researchers to make decisions in a more clinically relevant fashion.
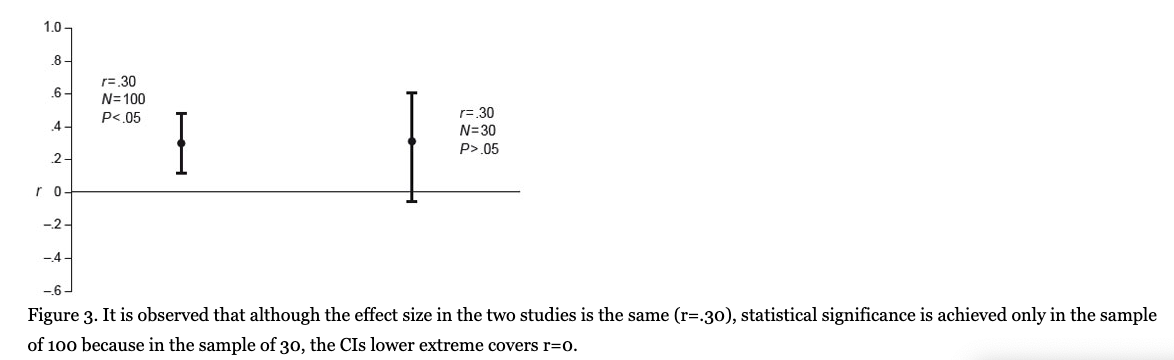
When we have, for example, r= .30 in a population of 100 subjects and we wish to obtain the respective confidence interval of that correlation coefficient in a population, selecting a confidence level of 95% (Z= 1.96), the external limits (confidence interval) of such a coefficient in the population are given as follows (see Figure 3):

In the population, this r value falls between +.11 and +.49. If it is a given that both limits are positive and the 95% confidence interval no contains zero, which is the parameter value specified in the null hypothesis, then the result is that r = .30 is statistically significant at the 0.05 level. However, if the r value was .30 but there was a smaller sample, for example, 30 persons, then the confidence intervals would be the following:
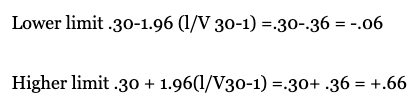
Here, the confidence interval is between -.06 and +.66 and the zero value is between the two limits; in this case, a correlation of .30 with N = 30 does not result in statistical significance. A population size of N = 30 requires a value of r = .35 to obtain statistical significance, and zero is not in the Cl range. As it is observed here, two studies can use the same intervention and find the same effect size, but only one can be statistically significant because of the size of the sample (Middel & Van Sonderen, 2002). The ES and its confidence interval, however, provide more information than the one offered only by the p value. When a researcher obtains a medium or large effect size but that size does not reach statistical significance, this finding indicates that there is an intervention effect and that the research needs only a higher sample size and/or minor variability. Conversely, if there is a very small ES and/or no clinical importance, but there is statistical significance, then it is probable that the sample size is notably large (see Figure 1). In conclusion, when a statistically significant value is obtained, the p value does not communicate whether this significance is due to the sample size or to the ES that is observed between two or more groups or variables (Nyirongo et al., 2008). For this reason, it is preferable to use the confidence interval on the effect size rather than the p value, which is a situation that the APA recognizes and recommends (APA, 2010): “Because confidence intervals combine information on location and precision and can often be directly used to infer significance levels, they are, in general, the best reporting strategy. The use of confidence intervals is therefore strongly recommended” (p. 34).
In spite of this APA recommendation, very few researchers report the effect size and its respective confidence intervals. Fritz, Morris, and Reichler (2012) analyzed studies that were published in the Journal of Experimental Psychology: General, during the period from 2009 to 2010 and found that less than half of the studies reported the effect size, and none of them reported the effect size with its respective confidence intervals.
Most statistical software packages include Cl results of statistical tests, but few packages calculate the effect size and their respective Cl, which would provide more complete and valuable information.
Statistical power
Statistical power refers to the ability of statistical tests to reject a null hypothesis when it really is false. In other words, statistical power is the probability of detecting a real effect when there really is an effect there to be found. Power reflects the
sensitivity of the test and is given by 1-/3, where jв is the probability of making a type II error (there are real differences, but the study is insufficiently powerful to detect them). By convention, .80 is an acceptable level of power indicating that there is an 80% chance of correctly detecting an effect if one genuinely exists (Cohen, 1992b). Statistical power depends on three factors: the effect size that you are looking for in the research, the sample size, and the alpha or p level. These factors are closely related; knowing the three values, we can obtain the test’s statistical power value.
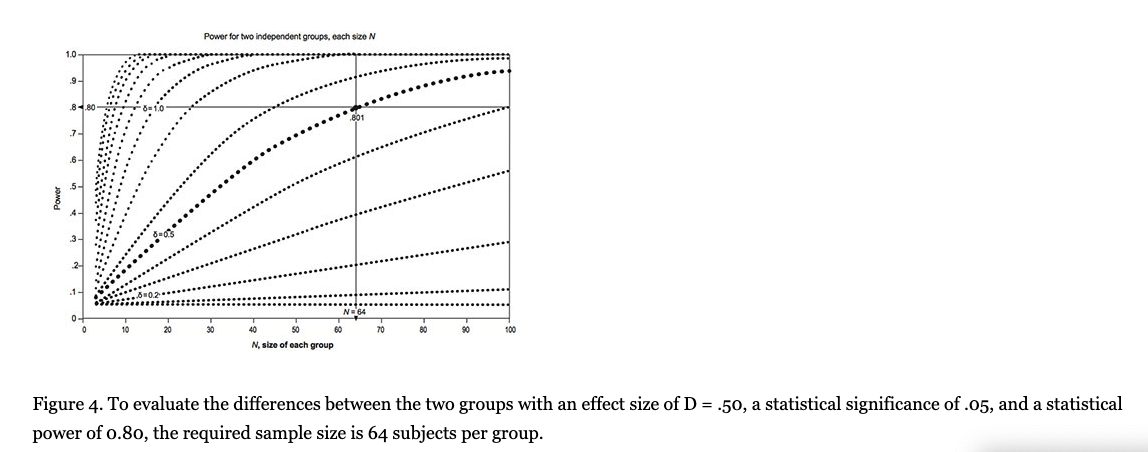
Let us suppose that we wish to research the effect of behavioral cognitive therapy for depression as measured by the Hospital Anxiety and Depression Scale (HADS), and the statistical significance criterion of p < .05 is proposed. Additionally, a minimum effect size of .50 is proposed, which is the ES that is considered to have the minimum clinical or practical importance (Norman, Sloan, & Wyrwich, 2003; Sloan, Celia, & Hays, 2005). Moreover, a power of .80 was recommended by Cohen (1992b). Under these criteria, a minimum sample of N = 64 is required in the intervention group and an equal number is required in the control group (see figure 4). If we set a criterion on the ES of .60 for practical significance, however, then we would need only 42 subjects per group, or if we decide on a criterion of a larger size, say .80, then we would require only N = 24. Therefore, increasing the sample size and/or effect size improves statistical power and precision by reducing the standard error of the effect size. Precision is reflected by the width of the confidence interval surrounding a given effect size. An effect size with a narrower Cl is more precise than a finding with a broader Cl.
The statistical power of .80 or /3=20 and a p value of .05 is four times more likely to produce a type II error than a type I error, and according to Cohen (1992a) is preferable to make a type II error than type I error. Cohen observed that most of the articles published in journals show a medium power of .47, even of .25, which indicates that the probability of making false decisions is very high. Cashen & Geiger (2004) discovered that only 9.3% of 43 studies analyzed the statistical power associated with the testing of null hypotheses, and the average statistical power of all studies was too small (.29). These authors note the following: “An important finding of this power assessment study was that explicit consideration of the power issue was almost nonexistent among researchers testing null hypotheses” (p. 161). In sum, many researchers are unaware of the statistical power of their studies and the consequences of low statistical power.
As we have shown, optimum statistical power (.80) is very important for generating knowledge. Failing to use an appropriate statistical power implies increasing the risk of obtaining false conclusions, rejecting the null hypothesis when it is not true (type I error) or accepting that there are no differences between groups when there truly are differences (type II error). Additionally, the lack of sufficient statistical power can provoke a waste of financial resources and even ethical problems because we are wasting patients’ time for research that a priori does not fulfill the requirements of a good study.
It is important to emphasize that the APA (2010) also exhorts authors to report statistical power: “When applying inferential statistics, take seriously the statistical power considerations associated with the tests of hypotheses. Such considerations relate to the likelihood of correctly rejecting the tested hypotheses, given a particular alpha level, effect size, and sample size. In that regard, routinely provide evidence that the study has sufficient power to detect effects of substantive interest” (p. 30). In spite of this recommendation, few scientific articles that are published report the statistical power.
Conclusions
The effect size is a useful statistical tool whose use is widely recommended by the American Psychological Association (1994,2001,2010), the American Educational Research Association (2006) (in the education field), and the International Committee of Medical Journal Editors (in the medical research area). Yet, few researchers follow the recommendations of these bodies when reporting their results. It is also important to recognize that an increasing number of psychology journal editors are demanding that authors report any type of ES and their confidence intervals. Hence, it is important to encourage the teaching, application and interpretation of ESs and their CIs in psychology graduate programs because researchers do not use them; the reason is usually that the researchers do not know about them or do not know how and when to use them (Rosnow, Rosenthal & Rubin, 2000). Moreover, ES use facilitates the use of results in meta-analytical research or the “study of studies” and consequently, the more efficient accumulation of psychological knowledge. Reporting ES and Cl also helps in reporting practical significance, which is essential in clinical research. Similarly, appropriate statistical power reduces the probability of drawing incorrect conclusions and prevents wasting financial resources that are dedicated to research.
Considering all of the foregoing information, beside NHST, it is important to encourage the use of ESs, their CIs and the appropriate use of statistical power in all of psychology research in graduate studies to enable new researchers to bring another perspective to the preparation, analysis, and interpretation of scientific data.
References
- Aiken, L. S., West, S. G., Sechrest, L., & Reno, R. R. (1990). Graduate trainingjn statistics, methodology, and measurement in psychology: A survey of PhD programs in North America. American Psychologist, 45, 721-734. doi: 10.1037/0003-066X.45.6.721
- Alhija, R N.-A., & Levy A. (2009). Effect size reporting practices in published articles. Educational and Psychological Measurement, 69(2), 245-265. doi: 10.1177/0013164408315266
- American Educational Research Association. (2006). Standards for Reporting on Empirical Social Science Research. Educational Researcher, 35 (6), 33-40. doi: 10.3102/0013189X035006033
- American Psychological Association. (1994). Publication Manual of the American Psychological Association (4th ed.). Washington, DC: Author.
- American Psychological Association. (2001). Publication Manual of the American Psychological Association (5th ed.). Washington, DC: Author.
- American Psychological Association. (2010). Publication Manual of the American Psychological Association. Washington, DC: Author.
- Camacho-Sandoval, J. (2007). Potencia estadistica en el diseno de estudios chnicos. Acta Medica Costarricense, 49 (4), 203-204.
- Cashen, L. H., & Geiger, S. W. (2004). Statistical power and the testing of null hypotheses: A review of contemporary management research and recommendations for future studies. Organizational Research Methods, 7(2), 151-167. doi: 10.1177/1094428104263676
- Clark, M. L. (2004). Los valores P у los intervalos de confianza: ^en que confiar?. Revista Pan-americana de Salud Pdblica/Pan American Journal of Public Health 15(5), 293-296. doi: 10.1590/S1020-49892004000500001
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale, NJ: Lawrence Earlbaum Associates.
- Cohen, J. (1994). The Earth is Round (p < .05). American Psychologist. 49(12), 997-1003. doi: 10.1037/0003-066X.49.12.997
- Cohen, J. (1992a). A power primer. Psychological Bulletin, 112(1), 155. doi:10.1037/0033-2909. 112.1.155
- Cohen, J. (1992b). Statistical power analysis. Current Directions in Psychological Science, 1(3), 98-101. Retrieved from http://www.jstor.org/stable/20182143 doi: 10.1111/1467-8721.epl0768783
- Cumming, G. (2014). The new statistics: Why and how. Psychological Science, 25. doi: 10.1177/0956797613504966
- Ferguson, C. J. (2009). An effect size primer: A guide for clinicians and researchers. Professional Psychology: Research and Practice, 40(5), 532. doi: I0.mi37/A0015808
- Freedman, К. B., Back, S., & Bernstein, J. (2001). Sample size and statistical power of randomised, controlled trials in orthopaedics. Journal of Bone & Joint Surgery, British Volume, 83(3), 397-402. doi: 10.1302/0301-620X.83B3.10582
- Frias, M, D., Pascual, L, J. & Garcia, J, F. (2000). Tamano del efecto del tratamiento у signification estadistica. Psicothema(12), 236-240. Retrieved from http://www.psicothema.com/pdf7555.pdf
- Fritz, C. O., Morris, R E., & Reichler, J. J. (2012).Effect size estimates: current use, calculations, and interpretation. Journal of Experimental Psychology: General, 141(1) 2-18. doi: 10.1037/ a0024338
- Grimes, D. A., & Schulz, K. F. (2002). An overview of clinical research: the lay of the land. The lancet, 359(9300), 57-61. doi: 10.1016/S0140-6736(02)07329-4
- Hemphill, J. F. (2003). Interpreting the magnitudes of correlation coefficients. American Psychologist, 58. doi: 10.1037/0003-066X.58.1.78
- Huberty, C. J. (2002). A history of effect size indices. Educational and Psychological Measurement, 62(2), 227-240. doi: 10.1177/0013164402062002002
- International Committee of Medical Journal Editors (2014) Recommendations for the conduct, reporting, editing, and publication of scholarly work in medical journals. Retrieved from www.icmje.org.
- Ivarsson, A., Andersen, M. B., Johnson, U., & Lindwall, M. (2013). To adjust or not adjust: Non-parametric effect sizes, confidence intervals, and real-world meaning. Psychology of Sport and Exercise, 14(1), 97-102. doi:10.1016/j.psychsport.2012.07.007
- Kirk, R. E. (2001). Promoting good statistical practices: Some suggestions. Educational and Psychological Measurement, 61(2), 213-218. doi: 10.1177/00131640121971185
- Kirk, R. E. (2007). Effect magnitude: A different focus. Journal of statistical planning and inference, 137(5), 1634-1646. doi: 10.1016/j.jspi.2006.09.011
- Maher, J. M., Markey, J. C., & Ebert-May, D. (2013). The other half of the story: Effect size analysis in quantitative research, CBE — Life Sciences Education, 12 (3), 345-351. doi: 10.1187/ cbe.13-04-0082
- Matthews, M. S., Gentry, M., McCoach, D. B., Worrell, F. C., Matthews, D., & Dixon, F. (2008). Evaluating the state of a field: effect size reporting in gifted education. The Journal of Experimental Education, 77(1), 55-65. doi: 10.3200/JEXE.77.1.55-68
- McMillan, J. H., & Foley, J. (2011). Reporting and discussing effect size: Still the road less traveled. Practical Assessment, Research & Evaluation, 16(14). Retrieved from http://pareonline.net/getvn.asp?v=168cn=14
- Middel, B., & Van Sonderen, E. (2002). Statistical significant change versus relevant or important change in (quasi) experimental design: some conceptual and methodological problems in estimating magnitude of intervention-related change in health services research. International Journal of Integrated Care, 2, 1-18. Retrieved from http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1480399/
- Morales-Vallejo, P. (2008) Estadistica aplicada a las Ciencias Sociales. Madrid: Universidad Pontificia Comillas.
- Norman, G. R., Sloan, J. A., у Wyrwich, K. W. (2003) Interpretation of changes in health-related quality of life: the remarkable universality of half a standard deviation. Medical Care, 41(5), 582-592. doi: 10.1097/01.MLR.0000062554.74615.4C
- Nyirongo, V. B., Mukaka, M. M., & Kalilani-Phiri, L. V. (2008). Statistical pitfalls in medical research. Malawi Medical Journal; 20 (1), 15-18. doi: 10.4314/mmj.v20il.10949
- Rosenthal, R., & Rubin, D. B. (2003). r equivalent: A simple effect size indicator. Psychological Methods, 8(4), 492. doi: 10.1037/1082-989X.8.4.492
- Rosenthal, R. (1994). Parametric measures of effect size. The Handbook of Research Synthesis. (pp. 232-243). New York: Russell and Sage Foundation.
- Rosnow, R. L., & Rosenthal, R. (1989). Statistical procedures and the justification of knowledge in psychological science. American Psychologist, 44(10), 1276. doi: 10.1037/0003. 066X.44.10.1276
- Rosnow, R. L., Rosenthal, R., & Rubin, D. B. (2000). Contrasts and correlations in effect-size estimation. American Psychological Society, 11(6): 446-453. doi: 10.1111/1467-9280.00287
- Schmidt, R, & Hunter, J. (2002). Are there Benefits From NHST? American Psychologist, 57. doi: 10.1037/0003-066X.57.1.65
- Schmidt, F. L. (1996). Statistical significance testing and cumulative knowledge in psychology: Implications for training of researchers, Psychological Methods, 1(2), 115. doi: 10.1037/1082- 989X.1.2.155
- Sloan, J. A., Celia, D., & Hays, R. D. (2005) Clinical significance of patient-reported questionnaire data: another step toward consensus, Journal of Clinical Epidemiology, 58(12), 1217- 1219. doi: 10.1016/j.jclinepi.2005.07.009
- Smith, M. L., & Glass, G. V. (1977). Meta-analysis of psychotherapy outcome studies. American Psychologist, 32(9)752. doi:10.1037/0003-066X.32.9.752
- Snyder, R, & Lawson, S. (1993). Evaluating results using corrected and uncorrected effect size estimates. The Journal of Experimental Education,61(4), 334-349. doi:10.1080/00220973.19 93.10806594
- Szumilas, M., (2010) Explaining Odds Ratios. Journal of the Canandian Acadademy of Child & Adolescent Psychiatry, 19(3), 227-229.
- Task Force on Reporting of Research Methods in AERA Publications. (2006). Standards for reporting on empirical social science research in AERA publications. Washington, DC: American Educational Research Association.
- Thomas, J. R., Salazar, W., & Landers, D. M. (1991). What is missing in p < .05? Effect size. Research Quarterly for Exercise and Sport, 62(3), 344-348. doi: 10.1080/02701367.1991.10608733
- Thompson, B. (2002). What future quantitative social science research could look like: Confidence intervals for effect sizes. Educational Researcher, 31(3), 25-32. doi: 10.3102/0013189X031003025
- Traftmow D. & Marks M. (2015) Editorial, Basic and Applied Social Psychology, 37:1,1-2, DOI: 10.1080/01973533.2015.1012991
- Tressoldi, P. E., Giofre, D., Sella, E, & Cumming, G. (2013). High Impact = high statistical standards? Not necessarily so. PloS One, 8(2), e56180. doi: 10.137 l/joumaLpone.0056180
- Wilkinson, L. & APA Task Force on Statistical Inference. (1999). Statistical methods in psychology journals: Guidelines and explanations, American Psychologist, 54(8), 594. doi:10.1037/0003-066X.54.8.594





