Research Problem

Creative problem solving is often accompanied by a feeling of illumination, which is known in the psychology of thinking as a phenomenon of insight. An aim of this study is the incubation phase of the thinking process, which is traditionally considered to precede insight. The questions of which cognitive processes precede illumination and why we need incubation are basic problems in the cognitive study of insight. A number of researchers believe that computational processes that may be qualified as transition procedures in a “search tree” occur during incubation (Newell & Simon, 1972). According to other authors, a clearing of irrelevant solutions from the working memory (Anderson, 2009), an active waiting for the right information (Seifert, Meyer, Davidson, Patalano, & Yaniv, 1995), as well as processes of active information processing (Davidson, 2003; Knoblich, Ohlsson, & Raney, 2001) can occur during the incubation.

Traditionally, the insight phenomenon is studied within the Gestalt approach to the psychology of thinking. Gestalt psychologists raised fundamental theoretical issues, in particular about the specifics of productive and reproductive thinking, the mechanisms of problem solving, the structure of the problem, etc. (Duncker, 1945; Köhler, 1917; Maier, 1931; Wertheimer, 1959). The main idea of this theory can be formulated as a statement about the role of holistic structures in the thinking process. Thus, it is not the individual elements of the problem situation, their properties and interrelations that become the focus of the research, but rather the phenomenal field, problem situation as such and the holistic structure of the problem. Finding an aspect of the object that is included in the context of the particular situation (“functional value” of the object) is postulated to be a means of problem solving. Insight is understood as a phenomenon which is based on a special creative process — restructuring of the phenomenal field (Köhler, 1917; Knoblich, Ohlsson, & Raney, 2001; Ohlsson, 1992).

The dominant theory in the cognitive psychology of problem solving has long been the problem space theory (Newell & Simon, 1972). The basic idea of this theory is the fact that any problem solving is a process of calculation on the basis of a set of elements of the problem, represented in the form of all possible states, a set of operators and the rules for their application. In this formulation, there is no specific “creative” process; there are only computational operations and heuristics of their most effective application (Kaplan & Simon, 1990). However, there are data that show both subjective differences in the solving of algorithmized and insight problems (Metcalfe & Wiebe, 1987) and procedural differences in the different types of solutions (Kounios & Beeman, 2009). In general, many cognitive studies of insight problem solving aimed to deny any specific mechanisms of insight (Weisberg & Alba, 1981) or to revive, configure and create a more sophisticated version of the problem space theory (MacGregor, Ormerod, & Chronicle, 2001; Ormerod, MacGregor, & Chronicle, 2002).

Some authors suggest that working memory plays an important role in the problem solving process (Anderson, 2009; Robertson, 2001; Ericsson & Simon, 1980). The following mechanisms of working memory are assumed to be involved in problem solving: the clearing of working memory that results in the advancement of a new hypothesis and insight solution (Anderson, 2009); the use of working memory in the process of solution verbalization (Ericsson & Simon, 1980); a shift of the working memory load when changing the representations in problem solving; and the limits of working memory resources, which hinders the solving of problems with the number of conditions exceeding the critical value (Hambrick & Engle, 2003).

Let us propose the types of dynamics of the working memory load which would correspond to different models of insight. In terms of the role of working memory in the phenomenon of insight, two alternative hypotheses are interesting. The first goes back to the works of Gestalt psychologists implemented, for example, in an opportunistic model (Seifert, Meyer, Davidson, Patalano, & Yaniv, 1995), involving unconscious processes at the stage of incubation. In this case, an increase in the working memory load at the stage of incubation can be observed. In the second hypothesis, the model of forgetting goes back to Woodworth (1938) and is supported by Anderson (2009). This hypothesis suggests a clearing of the working memory and forgetting of the wrong schemas, which allows a new trial to see the correct solution. According to this model, the opposite process can be observed — a decline of working memory load at the stage of incubation.

Among the most characteristic features of insight, the following are often referenced: a sudden solution (Jones, 2003), an original (creative) solution (Isen, Daubman, & Nowicki, 1987), thinking “outside the box” (Ohlsson, 1992), the presence of the incubation period (Segal 2004; Seifert, Meyer, Davidson, Patalano, & Yaniv, 1995), an “aha-reaction” (Kounios & Beeman, 2009), overcoming fixedness (Öllinger, Jones, & Knoblich, 2008), and finding functional solutions (Duncker, 1945). In our view, a critical feature for distinguishing insight and algorithmized solutions is the finding of functional solutions, which represents the selection of a new way to solve a problem (Duncker, 1945). All other referenced features are not constitutive for insight problem solving.

The solution and its nature depend on the structure of the problem (Duncker, 1945). We have proposed the traditional scheme of operationalization and actualization of thinking processes through the solving of various types of problems. We consider algorithmized problems as problems in which the system of operators and rules of their application are known (obvious or actualized), and the procedure for their solution can be described in terms of algorithms. Insight problems, in general, are problems which require a change of operators or the system of their application for the successful solution (finding a functional solution is required), and the new system of operators and rules is unknown (not obvious or not actualized) for the solver.

We assume that if the hypothesis about the specificity of insight problem solving processes is correct, then there are different processes in working memory during algorithmized and insight problem solving and, consequently, the dynamics of working memory load also differ. The hypothesis of our study can be formulated as follows: there are significant differences in the dynamics of working memory load in algorithmized and insight problem solving. Coincidence of the curves of working memory load, in our opinion, is an indication of the presence of common non-specific processes, while the difference between curves indicates the difference between problem solving processes.

Method

Numerous attempts to explore the issue of insight eventually encounter the problem of methodology. Difficulties are primarily associated with limitations of the classical methods which are able to discover the phenomenon of insight, but are not powerful enough to explore the microdynamics of thinking processes.

The microdynamics of problem solving processes (dynamics of solving within the same problem), in comparison with the microdynamics of other cognitive processes, is studied quite superficially. The phenomenological analysis of self-reports and descriptions of stages based on theoretical concepts dominate the literature on this issue (Duncker, 1945; Brushlinsky, 1979). Less frequently, researchers use the descriptions of stages based on analysis of the protocols of solving (Spiridonov, 2006) and the dynamics of the thinking process, based on additional indicators: an emotional reaction (Tikhomirov, 1969), eye movement (Knoblich, Ohlsson, Haider, & Rhenius, 1999), and a subjective assessment of proximity to a solution (Metcalfe & Wiebe, 1987). The first indicator seems to be historically reasonable for the period of psychological knowledge during which it was used; however, it has significant shortcomings — a search result is a foregone conclusion (empirical data are adjusted according to the authors concept), and it is impossible to make a description of the fine microdynamic mechanisms of the thinking process (features of the process at short time intervals). The combination of the second and the third indicators seems to us the most promising — the juxtaposition of verbal protocols (“thinking aloud” protocols or another way of objectification of the thinking process) with additional indicators. Selected indicators should be associated with the thought process.

The following are requirements for a research technique which explores the process dynamics during a problem solving, in our opinion. First, such a technique should make it possible to monitor the dynamics at the shortest possible time intervals (seconds to milliseconds) during the entire problem solving. Second, it must be relevant to solving processes which are hidden from direct observation. Third, the technique must not violate and distract from the natural thinking process.

Insight is described by researchers who support the idea of the specificity of its mechanisms as a phenomenon with an “instantaneous” nature (Duncker, 1945; Metcalfe & Wiebe, 1987; Ohlsson, 1992). Therefore, we can assume that it is based on very simple or very fast processes. These refinements impose some serious research methodology requirements, in particular, the quality of its temporal “resolution”. A number of studies attempted to assess the dynamics of the processes accompanying problem solving at various intervals: gaze fixation during problem solving at each of three periods of the duration of a trial (Knoblich, Ohlsson, & Raney, 2001), assessment of a feeling of proximity (“feeling of warmth”) to the solution at intervals of 15 seconds (Metcalfe & Wiebe, 1987), current change of galvanic skin response (GSR) at intervals of less than five seconds (Tikhomirov, 1969), or current change of EEG at intervals of less than 100 milliseconds (Kounios & Beeman, 2009). Despite attempts to use the assessment of the dynamics of the accompanying processes in solving problems, it is difficult to conclude anything about the mechanisms underlying thought processes.

The requirement of relevancy to problem solving is implemented in techniques of comparisons across intervals, self-report about operations and actual representation (e. g., Metcalfe & Wiebe, 1987; Ponomarev, 1976). They are based on the idea of the possibility of suspending the problem solving (or its fragmentation into smaller problems) in order to give self-reports about operations used in solving. However, these techniques operate with large time intervals and seriously disrupt the thought process. Moreover, the effectiveness and objectivity of a self-report is questionable.

One of the characteristics relevant to problem solving is the processes in working memory storage. The review of Hambrick and Engle (2003) examines the history of research of working memory in problem solving. These studies clearly show that this structure plays a significant role in the process of solving problems. Working memory is responsible for storing the actual representation of conditions and the course of transformations in the problem field by mental operations. However, these studies give no clue about working memory dynamics parameters, which are important for the disclosure of the dynamic laws of thought processes. As a way to compare different methodological approaches, Hambrick and Engle (2003) describe the European (procedural) tradition which often involves an experimental exploration of reciprocal distraction of two concurrent tasks (Baddeley & Hitch, 1974; Robbins et al., 1996) and the North American tradition of measuring the correlation between different types of tasks and working memory capacity (Daneman & Carpenter, 1980). Correlational works demonstrate the statistical relationship between parameters of working memory and problem solving efficiency. All experimental investigations that are carried out in the field use the dual task procedure, where a secondary task is used as a distractor (Gilhooly, Logie, Wetherick, & Wynn, 1993). The authors judged which one of the working memory structures is important for problem solving according to the type of effective distractor. It should be noted that a similar technique is to use an additional tool to facilitate problem solving, for example the use of hints during solving (Moss, Kotovsky, & Cagan, 2011; Ponomarev, 1976). These methods have a common weakness. They reveal the importance of each structure for a particular type of problem, but do not allow us to answer the question: do the structures have the same importance during all the stages of problem solving, or only at some of them? Overall, distractor tasks inhibit the process and facilitator tools improve it.

We suggest the use of working memory process monitoring during problem solving to make sure that the experimental procedure does not violate the natural thinking process. This technique was first proposed by Kahneman (1973) and was based on a limited resource model. One of the assumptions of this model is that the resource distribution during the execution of multiple confronted tasks is the following: the performance of secondary tasks suffers the most when the quality of the primary task is almost fully intact. This option, as well as the distractor task, can be viewed as a special case of dual task performance. However, there are significant differences. First, applying a general or particular type of resource that is used in the problem is indicated by the change of the secondary task parameters, but not the change of the quality of solutions or solution time. Second, such a secondary task, if it is quite simple, can be presented repeatedly in the process of problem solving (primary task), that will monitor the dynamics of the structures of working memory in the thought process. This type of dual task was named the “probe task' to distinguish it from the methodological technique “distractor task”.

The technique of “probing” the process can be performed in two ways. We define the first option as a “probe puncture” that involves a single probe presentation during the primary task. This “puncture” is performed at different time periods for each participant from the sample and allows us to construct curves of dynamics of the investigated parameters by the sample statistics. This design was used to carry out a number of investigations of Posner (Posner & Boies, 1971; Posner & Snyder, 1975). The hint presentation at the different stages of the thinking process is basically a similar strategy (Moss, Kotovsky, & Cagan, 2011). The second option was implemented by Kahneman (1973) and involves the parallel execution of the probe task during the performance
of the primary task. We define this as a “probe monitor”. The two-alternative choice task or the signal detection task can be used as such a monitor. This option, in our opinion, has significant advantages over the technique of the “probe puncture”. It can produce both group and individual curves of the dynamics of problem solving. It also provides the possibility to perform typological analysis of data and reduces the risk of artefact results.

Thus, based on the model of resource constraints, there may be various specific information processing systems (“storages”) with limited capacity. In this case, the dynamics of the primary task can be assessed by the dynamics of the secondary task performance because of competition for resources. Crashes, deceleration and errors in performance will indicate the maximum load of working memory by the solving of the primary task. A secondary task is required in this study: the dynamics of the primary intellectual problem solving is traced by the probe task performance. Using such a methodological technique, we can investigate the issue of incubation in problem solving: Are there specific mechanisms of insight problem solving which are fundamentally different from the processes of algorithmized problem solving?

Participants

The study sample consisted of 22 participants, aged 18 to 53 years. The study involved four men and 18 women: students, graduate students and people with higher education. All participated on a voluntary basis, without additional motivation.

Procedure

Working memory load acts as an indicator of the dynamics of cognitive mechanisms during problem solving. Measuring the dynamics of working memory load was carried out by the simultaneous performance of a two-altemative choice task and primary problem solving.

Statistical units are the average response time of each participant at each stage of the probe tasks. Statistical analysis was performed using one-way and two-way ANOVA with repeated measures.

Participants were asked to perform practice and control series of the two-alternative choice task, and to solve insight and algorithmized problems while performing the parallel two-alternative choice task. For an introduction to the experiment, a participant solved a problem that was not used in the main series. The practice series aimed for familiarization and training of the two-altemative choice task without parallel problem solving. In the control series, participants performed the two-alternative choice task for 90 seconds. The data from the control series are considered as a baseline of the working memory load by using a probe task. Furthermore, the dynamics of working memory load in a dual task performance were compared with this background.

The two-altemative choice task was chosen as the monitor-probe of working memory. Participants were asked to rapidly press the appropriate keys (“right” and “left” arrows) in response to a random on-screen presentation of green and red cards. In this case, the main load is in the central executive block in terms of the classical working memory model (Baddeley & Hitch, 1974). As a measure of working memory load, we used the dynamics of reaction time in the two-alternative choice task performance.

For the experimental series, various problems were selected as “insight problems” which demand a functional solution and are difficult to calculate step-by-step. Examples of insight problems include the following: “A famous psychic states that he is able to predict the score of any hockey game before the game begins. How is this possible?” (Solution: The starting score of any hockey game is 0 to 0); “The legendary runner Flash Fleetfoot was so fast that his friends said he could turn off the light switch and jump into bed before the room got dark. On one occasion Flash proved he could do it. How?” (Solution: He went to bed during the day); “The first received its name because of the size, the second prefers to be dressed, the third is known for its location, the fourth because of its ability to give additional information. How do we call the fifth?” (Solution: this problem is about fingers. The first is a little finger, the second is a ring finger, the third is a middle finger, and the fourth is an index finger. The fifth is a thumb¹ (This problem is culture-specific and thus it might be unclear in other cultures.) ).

Algorithmized problems are made according to the principle of incremental calculation. Examples of algorithmized problems include: “65x24-541” (Solution: 1, 019); “A father with two sons came to a wide river. The only way to get to the other side was to take a raft. However, the raft could carry only the father or his two sons. How does the family get to the other side?” (Solution: First go the sons. One son comes back, and father goes on the other side. Then second son goes back to pick his brother up and they both go to the other side); “Three chickens lay tree eggs in three days. How many eggs will 12 chickens lay in 12 days?” (Solution: 48).

Participants were asked to solve two problems from the set above with a parallel probe task, and then to solve two problems without the probe tasks. The sequence of problems was varied randomly by a computer program. The problems were equalized in complexity; the solution times of all problems in the condition without the probe tasks were not significantly different. The analysis excludes data from samples in which problems were not solved, problems which were solved faster than 30 seconds, when participants had at least one reaction time over nine seconds in the probe task, and when a response time was less than 50 milliseconds. In total, we excluded 23% (10 of 44) trials. Because the trials were eliminated unequally and, moreover, a participant could randomly receive two problems of one type, the final data were analyzed in sets of 13 insight and 26 algorithmized problems.

All problems were solved orally using the “think aloud” technique. Problems were presented on a computer monitor at the top of the screen; the text was available throughout the entire task performance. In the center of the screen, color images were presented as the stimuli for the probe task. A participant was instructed to independently solve a problem. In the case of an incorrect answer, the experimenter informed the participant about the wrong solution; in the case of a correct solution, the participant was told that the problem had been solved, and the task was interrupted.

It is possible to draw a graph for each participant in each trial which reflects the dynamics of the probe task performance across all time points at which reaction times were recorded. The comparison of task performance dynamics and the construction of generalized graphs can be based on absolute values (time remaining to a solution), or on relative values (stages of solving). Due to the time differences of problem solving, the time of every task was divided into 10 equal segments by means of which is possible to compare the dynamics of task performance in different participants. The number of stages is chosen rather arbitrarily, but guided by the requirement of a maximum fractionality. Traditionally in the psychology of problem solving, the dynamics of solving are considered in three or four stages (Knoblich, Ohlsson, & Raney, 2001; Moss, Kotovsky, & Lagan, 2011; Spiridonov, 2006). However, increasing the number of stages increases the response time requirements (a reaction time should not exceed the duration of the stage). Therefore, increasing the number of stages would increase exclusion of tasks. The dimension of the 10 stages was accepted as optimal.

Results

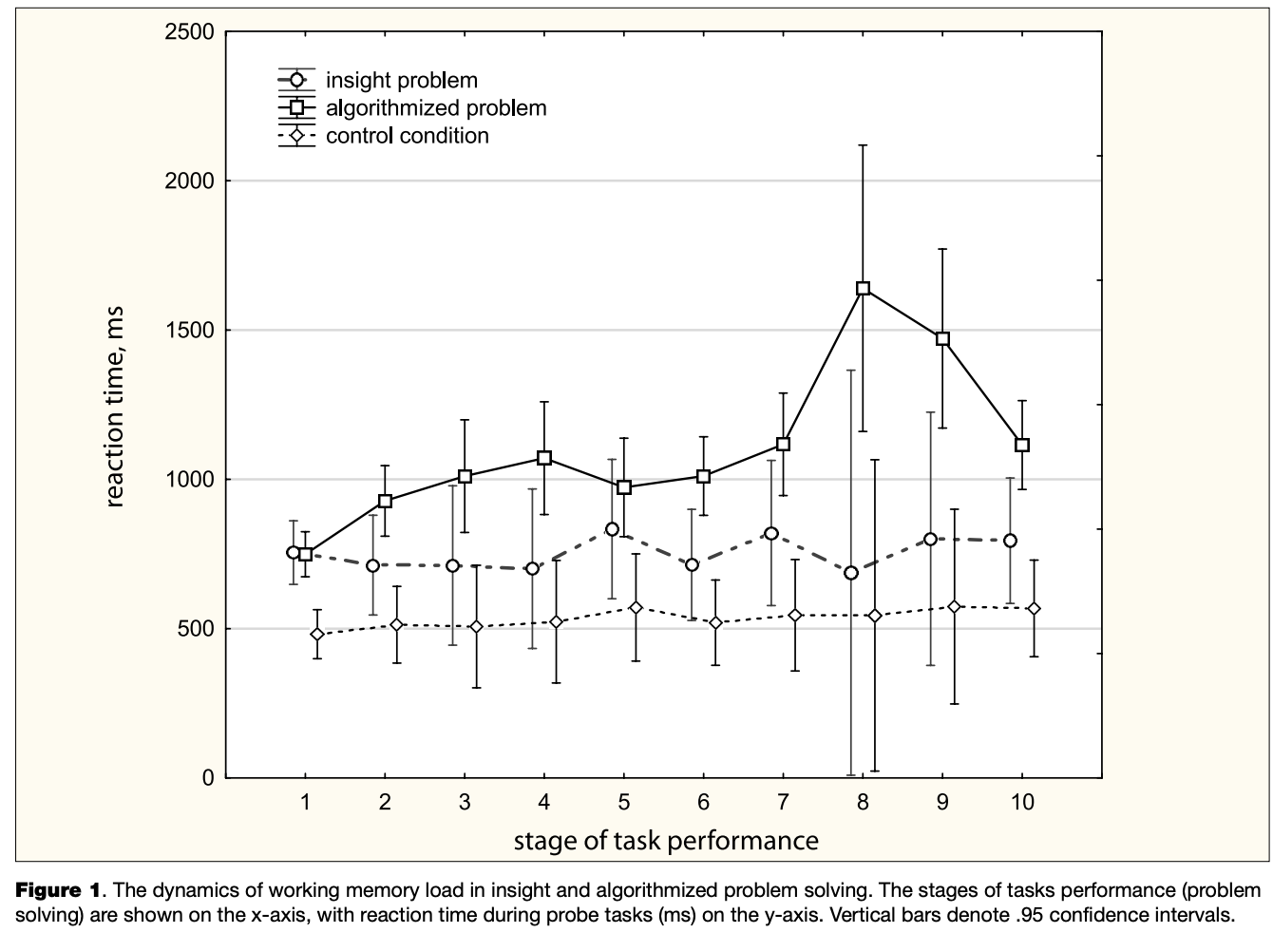
The following significant results of the study were obtained. The specificity of insight and algorithmized problem solving is reflected in the dynamics of working memory load for the three conditions (Figure 1).

We should note the following results. According to the one-way ANOVA with repeated measures, there are significant differences in the dynamics of working memory load between the control condition of the two-alternative choice task and the parallel performance of the probe task with insight (F(l, 350) = 30.5, pc.001, q_p² = .48) and algorithmized (F(l, 480) = 27.4, pc.001, q_p² = .37) problem solving. Probably, parallel tasks come into conflict for working memory’s limited resources.

As a result of the one-way ANOVA with repeated measures, we found the absence of dynamics of working memory load in insight problem solving (F(9, 130) = .70, p = .71, q_p² = .O6). The productivity of the probe task performance in the insight problem condition is higher than in the algorithmized problem condition (F(l, 390) = 6, p = .O19, q_p² = .14). Apparently, insight problem solving depends on the activation of resources that are not related to the two-alternative choice task processing.

We found the dynamics of working memory load in algorithmized problem solving (F (9,260) = 3.48, pc .001, q_p² = .12) using one-way ANOVA with repeated measures. The dynamics of algorithmized problem solving are manifested in the form of a “hump” closer to the problem solution. It should be noted that the problem solving dynamics coincide with the results of attention tasks (Kahneman & Beatty, 1966); there is a decrease of productivity with a consequent increase. Productivity peaks are associated with operations that require relatively little resources, such as the reading of conditions and the verbalization of a solution. The decrease of productivity that occurs close to the problem solution is associated with the implementation of algorithmized operations.

There is a significant interaction between factors of conditions and stages [insight, algorithmized problems, control condition x 10 stages] in the two-way ANOVA with repeated measures (J⁷(18, 610) =2.1, p< .01, q_p² = .O7). The results of the two-way ANOVA with repeated measures without a control condition [insight, algorithmized problems x 10 stages] show that there is no significant interaction between factors of conditions and stages (F(9,390) = 1.76, p = .07, q_p² = .05). The factor of conditions (problems) is significant — there are significant differences in the dynamics of working memory load in insight and algorithmized problem solving that occur in general productivity levels as well as in profiles of dynamics (F(l, 390) =6, p = .O19, q_p² = .14). Since the performance of the dual task compared with the control condition leads to a unilateral increase of complexity of the tasks, it is difficult to expect any cross-effect in the analysis of variance. It is unlikely that performing the dual task will increase the probe productivity compared to the control condition. The hypothesis about different mechanisms in algorithmized and insight problem solving can be verified by the differences in the dynamics of working memory load at different stages. To test this hypothesis, we split the data into two parts (stages 1-5 and stages 6-10). There are no significant differences between insight and algorithmized problems in the level of working memory load at the early stages (stages 1-5) of solving (F(l, 195) =3.07, p = .09, q_p² = .O8). However, we have found significant differences between the problems in the later stages (stages 6-10) of solving (F(l, 195) =6.7, p = .O14, q_p² = .15). It is likely that the different structures of working memory in insight and algorithmized problem solving are involved at the later stages of solving.

Discussion

The contrast between the experimental conditions (dual task) and the control condition (probe task) is connected with the fact that the probe task comes into competition for the limited resources of working memory structures. At the same time, competition does not disrupt the process of problem solving (all problems have been solved completely). These facts allow us to claim that the probe task meets the requirement of not violating the flow of the natural process, and can be used as a methodological approach to the study of processes in working memory related to thinking. In addition, the technique allows us to monitor the dynamics of working memory load with a time resolution of about one second (the average reaction time in the control condition was 535 ms; the average reaction time in the experimental conditions was 982 ms).

Turning to the results of this study, we can see that the hypothesis about significant differences between the dynamics of working memory load in insight and those of algorithmized problem solving is partially confirmed. There are differences in working memory load between problems at the last stages of solving. The early stages of problem solving are likely related to the reading and understanding of the problem conditions and require access to the same structures of the working memory. Maximum loading of working memory (“the hump”) can be observed in algorithmized problem solving, which peaks during the eighth stage of solving a problem. This “hump” can be observed within the period of maximal load of working memory when intermediate results of algorithmized problems are maintained. Similar results and interpretation can be found in studies using the probe tasks in attention tests (Kahneman, 1973). However, the dynamics of working memory load in insight problem solving is different. The curve of the dynamics of working memory load has no significant declines and increases, remaining at the same level throughout the time of problem solving.

In our view, the differences between problems at the last stages are an argument for a specific mechanism of insight problem solving. Manifestation of the dynamics of working memory load in algorithmized problem solving shows the relevance of the probe task to processes involved in the solving of this type of problem. At the same time, the fact that significant dynamics of reaction time in insight problem solving during the two-alternative choice task performing was not detected is interpreted as the irrelevancy of the selected probe to processes involved in insight problem solving.

On the one hand, simultaneous relevancy and irrelevancy of the probe to the problems of different types can show us that the various resources are involved in these problems. On the other hand, it is necessary to choose a specific probe which could demonstrate the specific dynamics in insight problem solving for the understanding of the nature of the insight processes. The selection of such a probe would allow us to formulate assumptions about the processes of problem solving and their stages which stand behind the phenomenon of incubation.

To find such a probe in the future we plan to vary probe tasks relative to their content and format of representation (imaginary and semantic), levels of information processing (low-level and high-level), the number of choice alternatives, emotional connotations of a probe, etc. Varying the probes is one attempt to narrow the search area of possible “insight processes”.

Conclusions

Our experimental study confirms the position of proponents of insight specificity. Our work shows the different dynamics of working memory load in insight and algorithmized problem solving at the last stages of solving. We have found the dynamics of working memory load in algorithmized problem solving via a probe task. The dynamics of working memory load in insight problem solving were not detected. The developed probe task technique can be useful for the investigation of the dynamics of problem solving processes. The proposed two-altemative choice task with two simple alternatives is relevant for detecting the algorithmized problem solving dynamics, but irrelevant to processes which are involved in insight problem solving. The main prospect of studies of this issue is the search for new probes that are relevant to the specific insight processes.

References

Anderson, J. R. (2005). Cognitive psychology and its implications. N. Y.: Macmillan. Baddeley, A.D., & Hitch, G. (1974). Working memory. In G. Bower (Ed.), Psychology of learning and motivation: Vol. 8 (pp. 47-89). N.Y: Academic Press.

Brushlinsky, A. (1979). [Thinking and forecasting]. Moscow: Mysl. (Russian).

Daneman, M., & Carpenter, P. A. (1980). Individual differences in working memory and reading. Journal of Verbal Learning and Verbal Behavior, 19(4), 450-466. doi: 10.1016/ 80022-5371(80)90312-6

Davidson, J. E. (2003). Insights about insightful problem solving. In J. E. Davidson, & R. E. Sternberg (Eds.), Thepsychol- ogy of problem solving (pp. 149-175). New York: Cambridge University Press, doi: 10.1017/CB09780511615771.006

Duncker, K. (1945). On problem-solving. Psychological Monographs, 58(5), 1-113. doi: 10.1037/h0093599

Ericsson, K.A., & Simon, H.A. (1980). Verbal reports as data. Psychological Review, 87(3), 215-251. doi: 10.1037/ 0033-295X.87.3.215

Gilhooly, K., Logie, R., Wetherick, N., & Wynn, V. (1993). Working memory and strategies in syllogistic-reasoning tasks. Memory & Cognition, 21(1), 115-124. doi: 10.3758/ BF03211170

Hambrick, D. Z., & Engle, R. W. (2003). The role of working memory in problem solving. In J. E. Davidson, & R. E. Sternberg (Eds.), The psychology of problem solving (pp. 176-206). N.Y: Cambridge University Press, doi: 10.1017/ CBO978Q511615771.007

Isen, A.M., Daubman, K. A., & Nowicki, G.P. (1987). Positive affect facilitates creative problem solving. Journal of Personality and Social Psychology, 52(6), 1122-1131. doi: 10.1037/0022-3514.52.6.1122

Jones, G. (2003). Testing two cognitive theories of insight. Journal of Experimental Psychology: Learning Memory, and Cognition, 29(5), 1017-1027. doi: 10.1037/0278-7393.29.5.1017

Köhler, W. (1917). Intelligenzprüfungen an Anthropoiden. Berlin: Verlag der Königlichen Akademie des Wissens.

Kahneman, D. (1973). Attention and effort. Englewood Cliffs, New Jersey: Prentice Hall Inc.

Kahneman, D., & Beatty, J. (1966). Pupil diameter and load on memory. Science, 154(3756), 1583-1585. doi: 10.1126/ science. 154,3756.1583

Kaplan, C.A., & Simon, H.A. (1990). In search of insight. Cognitive Psychology, 22(3), 374-419.

Knoblich, G., Ohlsson, S., Haider, H., & Rhenius, D. (1999). Constraint relaxation and chunk decomposition in insight problem solving. Journal of Experimental Psychology: Learning, Memory, and Cognition, 25(6), 1534-1555. doi: 10.1037/0278-7393.25.6.1534

Knoblich, G., Ohlsson, S., & Raney, G.E. (2001). An eye movement study of insight problem solving. Memory & Cognition, 29(7), 1000-1009. doi: 10.3758/BF03195762

Kounios, J., & Beeman, M. (2009). The Aha! moment: The cognitive neuroscience of insight. Current Directions in Psychological Science, 18(4), 210-216. doi: 10.1111/ i. 1467-8721.2009.01638.x

MacGregor, J.N., Ormerod, T.C., & Chronicle, E.P. (2001). Information processing and insight: A process model of performance on the nine-dot and related problems. Journal of Experimental Psychology: Learning Memory, and Cognition, 27(1), 176-201. doi: 10.1037//0278-7393.27.1.176

Maier, N. R. (1931). Reasoning in humans. II. The solution of a problem and its appearance in consciousness. Journal of Comparative Psychology, 12(2), 181-194. doi: 10.1037/ h0071361

Metcalfe, J., & Wiebe, D. (1987). Intuition in insight and noninsight problem solving. Memory & Cognition, 15(3), 238-246. doi: 10.3758/BF03197722

Moss, J., Kotovsky, K., & Cagan, J. (2011). The effect of incidental hints when problems are suspended before, during, or after an impasse. Journal of Experimental Psychology: Learning Memory, and Cognition, 37(1), 140-148. doi: 10.1037/ a0021206

Newell, A., & Simon, H.A. (1972). Human problem solving. Englewood Cliffs, NJ: Prentice-Hall.

Ohlsson, S. (1992). Information-processing explanations of insight and related phenomena. In M. Keane, & K. Gilhooly (Eds.), Advances in the psychology of thinking: Vol. 1 (pp. 1-44). London: Harvester Wheatsheaf.

Öllinger, M., Jones, G., & Knoblich, G. (2008). Investigating the effect of mental set on insight problem solving. Experimental Psychology, 55(4),   269-282.

doi: 10.1027/1618-3169.55.4.269

Ormerod, T. C., MacGregor, J. N., & Chronicle, E. P. (2002). Dynamics and constraints in insight problem solving. Journal of Experimental Psychology: Learning Memory, and Cognition, 28(4), 791-799. doi: 10.1037/0278-7393.28.4.791

Ponomarev, YA. (1976). [Psychology of creativity]. Moscow: Nauka. (Russian).

Posner, M.I., & Boies, S. J. (1971). Components of attention. Psychological Review, 78(5), 391-408. doi: 10.1037/h0031333

Posner, M.I., & Snyder, C. (1975). Attention and cognitive control. In R. Solso (Ed.), Information processing and cognition: The Loyola symposium (pp. 55-85). Hillsdale, N. J.: Lawrence Erlbaum Associates.

Robbins, T, Anderson, E. J., Barker, D., Bradley, A., Fearny- hough, C., Henson, R., Hudson, S., & Baddeley, A. (1996). Working memory in chess. Memory & Cognition, 24(1), 83-93. doi: 10.3758/BF03197274

Robertson, S.I. (2001). Problem solving. Philadelphia: Psychology Press, doi: 10.4324/9780203457955

Segal, E. (2004). Incubation in insight problem solving. Creativity Research Journal, 16(1), 141-148. doi: 10.1207/ s!5326934crjl601 13

Seifert, C.M., Meyer, D. E., Davidson, N., Patalano, A. L., & Yaniv, I. (1994). Demystification of cognitive insight: Opportunistic assimilation and the prepared-mind hypothesis. In R. Sternberg, & J. Davidson (Eds.), The nature of insight (pp. 65-124). Cambridge: MIT Press.

Spiridonov, VF. (2006). [The psychology of thinking: Problem solving]. Moscow: Genesis. (Russian).

Tikhomirov, O.K. (1969). [The structure of human thinking activity]. Moscow: MSU. (Russian).

Weisberg, R.W, & Alba, J.W (1981). An examination of the alleged role of “fixation” in the solution of several “insight” problems. Journal of Experimental Psychology: General, 110(2), 169-192. doi: 10.1037/0096-3445.110.2.169

Wertheimer, M. Wertheimer, M. (Ed.). (1959). Productive thinking. New York: Harper & Row.

Woodworth, R. (1938). Experimental Psychology. New York: Holt.